Юрий Ревич - Занимательная микроэлектроника

Правила двоичной арифметики значительно проще, чем десятичной, и включают две таблицы — сложения и умножения — несколько похожие на те же таблицы для логических переменных:

0 + 0 = 0 0∙0 = 0

0 + 1 = 1 0∙1 = 0

1 + 0 = 1 1∙0 = 0

1 + 1 = 10 1∙1 = 1

Как мы видим, правила обычного умножения одноразрядных двоичных величин совпадают с таковыми для логического умножения. Однако правила сложения отличаются, т. к. при сложении двух единиц результат равен 2 и у нас появляется перенос в следующий разряд. Так как умножение многоразрядных чисел сводится к сложению отдельных произведений, то там придется этот перенос учитывать (как это делается на практике, мы увидим при рассмотрении микроконтроллеров).

Возможно, вы удивитесь, но любая электронная схема (и микропроцессор не исключение) умеет только складывать. Свести умножение к сложению легко. А как свести к сложению вычитание и деление? Для этого придется познакомиться с тем, как в электронике представляют отрицательные числа.

Отрицательные числа

Самый простой метод представления отрицательных чисел — отвести один бит (логичнее всего старший) для хранения знака. По причинам, которые вы поймете далее, значение «1» в этом бите означает знак «минус», а «0» — знак «плюс». Как будут выглядеть двоичные числа в таком представлении?

В области положительных чисел ничего не изменится, кроме того, что их диапазон сократится вдвое: например, для числа в байтовом представлении вместо диапазона 0—255 мы получим всего лишь 0—127 (0000 0000–0111 1111). А отрицательные числа будут иметь тот же диапазон, только старший бит у них будет равен единице. Все просто, не правда ли?

Нет, неправда. Такое представление отрицательных чисел совершенно не соответствует обычной числовой оси, на которой влево от нуля идет минус единица, а затем числа по абсолютной величине увеличиваются. Здесь же мы получаем, во-первых, два разных нуля («обычный» 0000 0000, и «отрицательный» 1000 0000), во-вторых, оси отрицательных и положительных чисел никак не стыкуются, и выполнение арифметических операций превратится в головоломку. Поэтому поступим так: договоримся, что -1 соответствует число 255 (1111 1111), — 2 — число 254 (1111 1110) и т. д., вниз до 128 (1000 0000), которое будет соответствовать -128 (и общий диапазон всех чисел получится от -128 до 127). Очевидно, что если вы в таком представлении хотите получить отрицательное число в обычном виде, то надо из значения числа (например, 240) вычесть максимальное значение диапазона (255) плюс 1 (256). Если отбросить знак, то результат такого вычитания (16 в данном случае) называется еще дополнением до 2 (или просто дополнительным кодом ) для исходного числа (а само исходное число 240 тогда будет дополнением до 2 для 16). Название «дополнение до 2» используется независимо от разрядности числа, потому что верхней границей всегда служит степень двойки (в десятичной системе аналогичная операция называется «дополнение до 10»).

Вычитание

Что произойдет в такой системе, если вычесть, например 2 из 1? Запишем это действие в двоичной системе обычным столбиком:

00000001

— 00000010

В первом разряде результата мы без проблем получаем 1, а уже для второго нам придется занимать 1 из старших, которые сплошь нули, поэтому представим себе, что у нас будто бы есть девятый разряд, равный 1, из которого заем в конечном итоге и происходит:

(1) 00000001

— 00000010

-

11111111

На самом деле девятиразрядное число 1 0000 0000 есть не что иное, как 256, т. е. то же самое максимальное значение +1, и мы здесь выполнили две операции: прибавили к вычитаемому эти самые 256, а затем выполнили вычитание, но уже в положительной области для всех участвующих чисел. А что результат? Он будет равен 255, т. е. тому самому числу, которое, как мы договорились, представляет собой -1. Таким образом, вычитание в такой системе происходит автоматически правильно, независимо от знака участвующих чисел.

Немного смущает только эта самая операция нахождения дополнения до 2, точнее, в данном случае до 256 — как ее осуществить на практике, если схема всего имеет 8 разрядов? В дальнейшем мы увидим, что на практике это не нужно: при вычитании и в микроконтроллерах, и в обычных электронных счетчиках все осуществляется автоматически.

Впрочем, в микропроцессорах есть обычно и отдельная команда, которая возвращает дополнение до 2. В большинстве ассемблеров она называется neg, от слова «негативный», потому что просто-напросто меняет знак исходного числа, если мы договариваемся считать числа «со знаком». Разберем из любопытства, как ее можно было бы осуществить «вручную», не обращаясь в действительности к 9-му разряду. Для этого выпишем столбиком какое-нибудь число (далее для примера — 2 и 240), результаты операции нахождения его дополнения до 2, и результат еще одной манипуляции, которая представляет собой вычитание единицы из дополнения до 2, или, что то же самое, просто вычитания исходного числа из наивысшего числа диапазона (255):

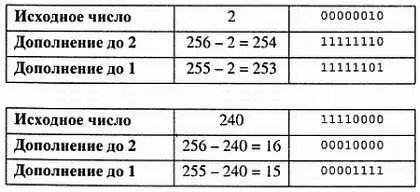
Если мы сравним двоичные представления в верхней и нижней строках в каждом случае, то увидим, что они могут быть получены друг из друга путем инверсии каждого из битов. Эта операция называется нахождением обратного кода или дополнения до единицы (потому что число, из которого вычитается, содержит все 1 во всех разрядах; для десятичной системы аналогичная операция называется «дополнение до 9»). Для нахождения дополнения до 1 девятый разряд не требуется, да и схему можно построить так, чтобы никаких вычитаний не производить, а просто «переворачивать» биты. Так и делается, конечно, но не ищите в микроконтроллерах специальной операции инверсии битов — для этого вызывается именно команда нахождения дополнения до 1 (в AVR-ассемблере она обозначается, как сом, и определяется, как операция вычитания из FFh, а что уж там происходит на самом деле — тайна, покрытая мраком). Итак, для полного сведения вычитания к сложению надо проделать три операции:

1. Найти дополнение до 1 для вычитаемого (инвертировать его биты).

2. Прибавить к результату 1, чтобы найти дополнение до 2.

3. Сложить уменьшаемое и дополнение до 2 для вычитаемого.

Заметки на полях

Заметим, что все сложности с этими многочисленными дополнениями связаны с наличием нуля в ряду натуральных чисел — если бы его не было, дополнение было бы всего одно, и операция вычитания упростилась. Так может греки все же были в чем-то правы?

В заключение обратим внимание на еще одно замечательное свойство двоичных чисел, которое часто позволяет значительно облегчить операции умножения и деления: а именно умножению на 2 соответствует операция сдвига всех разрядов числа на один разряд влево, а операции деления на 2 — вправо. Крайние разряды (старший при умножении и младший при делении) в общем случае при этом должны теряться, но в микропроцессорах есть специальный регистр, в один из битов которого ( бит переноса ) эти «потерянные» разряды помещаются. Противоположные крайние разряды (младший при умножении и старший при делении) в общем случае замещаются нулями, но могут замещаться значением бита переноса, что позволяет без лишних проблем делить и умножать числа с разрядностью больше одного байта. Как можно догадаться, умножению и делению на более высокие степени двойки будет соответствовать операция сдвига в нужную сторону на иное (равное степени) число разрядов. Излишне говорить, что операцию сдвига разрядов в электронных схемах производить неизмеримо проще, чем операции деления и умножения. Тот же самый бит переноса используется для размещения переноса в старший разряд при сложении и займа при вычитании.