Юрий Ревич - Занимательная микроэлектроника

Наоборот, идеальный источник тока , как нетрудно догадаться, обязан обладать бесконечным внутренним сопротивлением — только тогда ток в цепи совсем не будет зависеть от нагрузки. Понять, как источник реального тока (не бесконечно малого) может обладать бесконечным выходным сопротивлением, довольно трудно, и в быту таких источников вы не встретите. Однако уже обычный резистор, включенный последовательно с источником напряжения (не тока!), как R1 на рис. 1.3, при условии, что сопротивление нагрузки мало (R2 << R1), может служить хорошей моделью источника тока. Еще ближе к идеалу транзисторы в определенном включении, и мы с этим разберемся позднее.

Источники напряжения и тока обозначаются на схемах так, как показано на рис. 1.4, а и б . Не перепутайте, логики в этих обозначениях немного, но так уж принято. А эквивалентные схемы (их еще называют схемами замещения ) реальных источников приведены на рис. 1.4, в и г , где R Bобозначает внутреннее сопротивление источника. Как можно использовать эти эквивалентные схемы при анализе реальных цепей? Для этого нужно окончательно разобраться, как рассчитываются схемы с параллельным и последовательным включением резисторов.

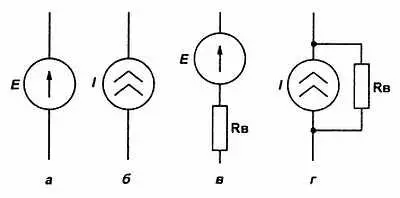
Рис. 1.4. Источники тока и напряжения:

а— обозначение идеального источника напряжения; б— обозначение идеального источника тока; в— эквивалентная схема реального источника напряжения; г— эквивалентная схема реального источника тока

Схемы постоянного тока любой степени сложности всегда можно представить как совокупность резисторов и идеальных источников напряжения и тока. Для их расчета достаточно знать два очень простых закона, названных по имени физика XIX столетия Густава Роберта Кирхгофа (1824–1887).

Первый закон Кирхгофа формулируется так: алгебраическая сумма токов в любом узле электрической цепи равна нулю . Или еще проще: сумма токов, направленных к данному узлу, равна сумме токов, направленных от него.

По сути он представляет одну из форм физических законов сохранения — ведь заряды не могут возникнуть из ничего, соответственно, сколько прибыло зарядов в некую точку, столько из нее обязано уйти.

Второй закон Кирхгофа гласит: алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю . Его легко проиллюстрировать на примере нашей схемы рис. 1.3 — там сумма падений напряжений на всех резисторах (включая внутреннее сопротивление батарейки, сопротивление амперметра, которым мы пренебрегали, и т. д.) равна напряжению батарейки. Иначе и быть не может— куда оно, напряжение батарейки, тогда денется?

Из законов Кирхгофа вытекают очень часто применяющиеся на практике правила последовательного и параллельного соединения резисторов: при последовательном соединении складываются сопротивления резисторов, а при параллельном складываются их проводимости, которые по определению, данному ранее, есть величины, обратные сопротивлению (рис. 1.5). Понять, почему правила именно таковы, можно, если рассмотреть течение токов в обоих случаях.

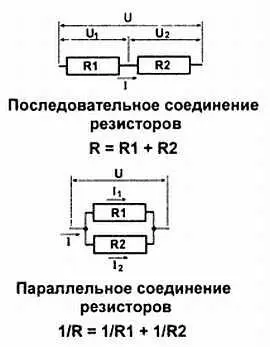
Рис. 1.5. Последовательное и параллельное соединение резисторов

• При последовательном соединении ток I через резисторы один и тот же, поэтому падения напряжения на них складываются ( U= U 1+ U 2), что равносильно сложению сопротивлений.

• При параллельном соединении, наоборот, равны падения напряжений U , а складывать приходится токи ( I= I 1+ I 2), что равносильно сложению проводимостей. Если вы не поняли сказанное, то посидите над рис. 1.5 с карандашом и бумагой и выведите выражения закона Ома для каждого из резисторов — и все станет на свои места.

Из этих определений вытекает также несколько практических правил, которые полезно заучить:

• При последовательном соединении:

— сумма двух резисторов имеет сопротивление всегда больше, чем сопротивление резистора с большим номиналом (правило «больше большего»);

— если номиналы резисторов равны, то суммарное сопротивление окажется вдвое больше каждого номинала;

— если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно большему номиналу. Типичный случай: в примере на рис. 1.3 мы игнорируем сопротивления проводов и амперметра, т. к. они много меньше сопротивлений резисторов.

• При параллельном соединении:

— сумма двух резисторов имеет сопротивление всегда меньше, чем сопротивление резистора с меньшим номиналом (правило «меньше меньшего»);

— если номиналы резисторов равны, то суммарное сопротивление будет вдвое меньше каждого номинала;

— если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно меньшему номиналу. Это также можно иллюстрировать на примере рис. 1.3, где мы игнорируем наличие вольтметра, включенного параллельно R2, т. к. его сопротивление намного больше сопротивления резистора.

Знание этих правил поможет вам быстро оценивать схему, не занимаясь алгебраическими упражнениями и не прибегая к помощи калькулятора. Даже если соотношение сопротивлений не попадает под перечисленные случаи, результат все равно можно оценить «на глаз» с достаточной точностью. При параллельном соединении, которое представляет большую сложность при расчетах, для такой оценки нужно прикинуть, какую долю меньшее сопротивление составляет от их арифметической суммы — именно во столько раз приблизительно снизится их общее сопротивление по отношению к меньшему.

Проверить это легко: рассмотрим ситуацию, когда сопротивления равны. В этом случае одно сопротивление составляет 1/ 2часть их суммы, т. е. общее сопротивление должно снизиться вдвое, как и есть на самом деле. Возьмем более сложный случай: одно сопротивление пусть имеет номинал 3,3 кОм, второе — 6,8 кОм. В соответствии с изложенным мы будем ожидать, что общее сопротивление должно быть на 30 % меньше, чем 3,3 кОм, т. е. 2,2 кОм (3,3 составляет примерно одну треть от суммы 3,3+6,8, т. е. общее сопротивление должно быть меньше, чем 3,3, на треть от этого значения, равную 1,1 — в результате и получаем 2,2 кОм). Если мы проверим результат, полученный такой прикидкой в уме, точным расчетом, то мы получим в результате 2,22 кОм, что очень неплохо.

В большинстве случаев нам такой точности и не потребуется — помните, что и сами сопротивления имеют разброс по номиналу, и для обычных схем допуски на номиналы стандартных компонентов могут быть довольно значительными (по крайней мере, в правильно составленных схемах). Если же схема в некоторых случаях должна все же иметь какие-то строго определенные параметры, то с помощью стандартных компонентов вы все равно этого не добьетесь, т. к. параметры, образно выражаясь, будут «гулять» (в пределах допусков, естественно) от дуновения ветерка из форточки. В таких случаях надо применять прецизионные резисторы и конденсаторы, а во времязадающих цепях использовать кварцевые резонаторы. Но составлять схему так, чтобы она теряла работоспособность от замены резистора 1 кОм на 1,1 кОм— не наш метод!