В Бессонов - Радиоэлектроника для начинающих (и не только)

Обратите внимание: общая емкость при последовательном соединении конденсаторов вычисляется по формуле, аналогичной формуле для вычисления общего сопротивления при параллельном соединении резисторов, а общая емкость при параллельном соединении конденсаторов — по формуле, аналогичной формуле для вычисления общего сопротивления при последовательном соединении резисторов.

Для получения необходимой емкости при последовательном соединении конденсаторов требуются некоторые вычисления. Для облегчения подбора ёмкости второго конденсатора (при известном значении емкости первого) на рис. 2.22 ( глава 2 ) приведена номограмма.

Как пользоваться номограммой? При определении общих параметров деталей, номиналы которых имеют один порядок, пользуются шкалами ОА, ОВ, ОС , а если номиналы различаются на один порядок, то шкалами ОА, OD, ОЕ . Поясним это на примерах.

• Пример 1. Последовательно соединены конденсаторы емкостью 5 и 20 мкФ. Чему равна общая емкость? Приложив линейку к делению 5 на шкале ОА и к делению 20 на шкале OD , на шкале ОЕ прочтем результат — 4 мкФ.

• Пример 2 . Какой емкости конденсатор необходимо включить последовательно с конденсатором емкостью 5,6 пФ, чтобы их общая емкость была 2,5 пФ? Прикладывая линейку к делениям 5,6 на шкале ОА и 2,5 на шкале ОС , на шкале ОВ прочтем — 4,5 пФ.

Чтобы лучше понять принцип работы конденсатора и катушки индуктивности как реактивных элементов, рекомендуем вам самостоятельно провести ряд простых экспериментов.

3.2.1. Конденсатор как накопитель электрической энергии

Для этого соберите схему (рис. 3.12, а ). В положении переключателя SA, указанного на рисунке, конденсатор С будет заряжаться от батареи. Ток заряда протекает по цепи: «+» батареи GB резистор R —> переключатель SA —> конденсатор С —> «—» батареи GB. Через несколько секунд конденсатор зарядится и можно переключатель SA поставить в правое положение, лампочка кратковременно вспыхнет и погаснет. Чтобы лучше уяснить процесс заряда и разряда конденсатора, воспользуемся аналогией. Представим конденсатор в виде сосуда с крышкой, который может вместить определенное количество жидкости, например бензина.

После заполнения этого сосуда бензин можно вылить и поджечь, — это эквивалентно вспышке лампочки.

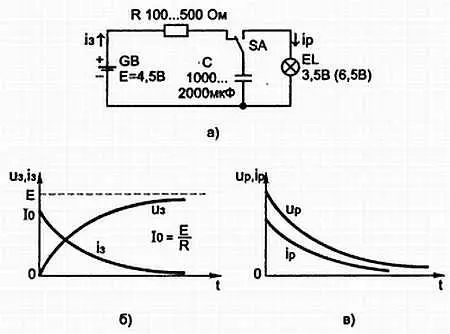
Рис. 3.12. а) Конденсатор — накопитель электрической энергии; б) График заряда конденсатора, в)график разряда конденсатора.

Для чего нужен резистор R в схеме рис. 3.12, а ? Если его не будет, то в момент подключения батареи к конденсатору ток заряда будет очень большим, конденсатор может взорваться от нагрева . Резистор R ограничивает ток заряда конденсатора. Конденсатор с хорошим диэлектриком может хранить заряд несколько суток; бумажные конденсаторы разряжаются почти полностью за несколько часов.

На рис. 3.12, б изображен график заряда конденсатора, а на рис. 3.12, в — график разряда конденсатора.

Емкость конденсаторов измеряется в фарадах (Ф), в микрофарадах (мкФ), нанофарадах (нФ), пикофарадах (пФ).

3.2.2. Конденсатор «не пропускает» постоянный ток

При замыкании выключателя SA (рис. 3.13, а ) лампочка кратковременно вспыхивает и гаснет. Это значит, что конденсатор не пропускает постоянный ток. Но из эксперимента можно сделать и другой вывод: в момент подключения батареи GB (замыкание выключателя SA ), когда напряжение на конденсаторе скачком увеличивается от нуля до 4,5 В, он не оказывает никакого сопротивления (т. е. его сопротивление в начальный момент равно нулю, все напряжение батареи приложено к лампе, сила тока максимальная). Со временем сила тока уменьшается и затем вовсе становится равной нулю. В этот момент конденсатор можно считать заряженным.

На рис. 3.13, б показан график зависимости силы тока, протекающего через конденсатор С и лампу накаливания EL , от времени, т. е. график заряда конденсатора. Из графика видно, что в момент замыкания выключателя SA (при t = 0) сила тока через лампу максимальная и равна I 0= E/ R л ~= 0,3 А.

Здесь R л= 14 Ом — сопротивление нити накала лампы.

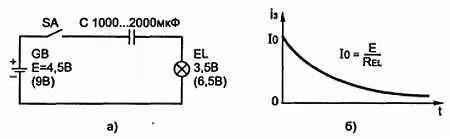
Рис. 3.13. а)Конденсатор не пропускает постоянный ток; б)График зависимости силы тока, протекающего через конденсатор Си через лампу накаливания EL

3.2.3. Сопротивление конденсатора переменному току зависит от его емкости и частоты тока

Меняя емкость конденсатора (рис. 3.14), можно убедиться, что лампа будет светиться по-разному. Для этого надо два конденсатора по 10 мкФ соединить параллельно, последовательно с ними включить лампочку EL на 3,6 В, на вход подать переменное напряжение 36 В. Зафиксировать яркость свечения лампочки. Затем подключить к этим конденсаторам параллельно еще один емкостью 5 мкФ и снова зафиксировать яркость свечения лампочки, — она увеличится. Отсюда вывод: с увеличением емкости конденсатора его сопротивление уменьшается. Обратите внимание, что все конденсаторы в этом эксперименте должны иметь рабочее напряжение не менее 60 В.

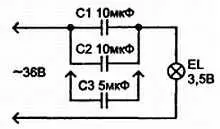
Рис. 3.14. Сопротивление конденсатора переменному току зависит от его ёмкости

Реактивное емкостное сопротивление конденсатора переменному току определяется по формуле:

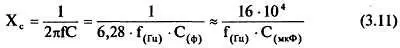
Тогда закон Ома запишется так:

I m= U m/ X c= 2 U mπ fC= U mω C. (3.12)

1 Ф = 10 6мкФ = 10 12пФ, 1 мкФ = 10 3нФ = 10 6пФ.

3.2.4.Сила тока опережает напряжение на емкости на угол π /2

Так как i= I mSin ωt , a u= U mSin ( ωt + π /2) то, следовательно, напряжение на конденсаторе отстает от силы тока по фазе на угол π/2 . Это видно на векторной (рис. 3.15, а ) и на временной (рис. 3.15, б ) диаграммах. Физически это можно понимать так: пока через конденсатор не потечет ток, на его пластинах не появятся заряды, до тех пор на пластинах и не будет напряжения.

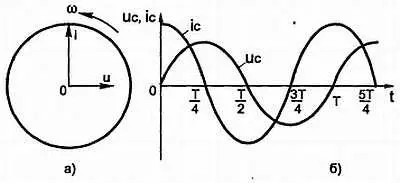
Рис. 3.15. Напряжение на конденсаторе отстаёт от силы тока по фазе на угод 90°