В Бессонов - Радиоэлектроника для начинающих (и не только)

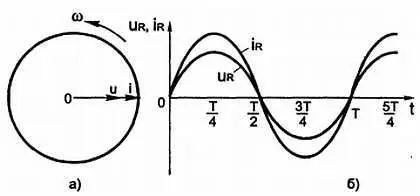
Рис. 3.23. Напряжение на резисторе совпадает по фазе с силой тока

В электронных устройствах часто бывает необходимо изменить прямоугольные импульсы или сигналы другой формы таким образом, чтобы получить сигнал требуемой формы. Указанное изменение может заключаться в сохранении высокочастотных составляющих сигнала и ослаблении низкочастотных составляющих, в ослаблении только высокочастотных составляющих, в изменении амплитуды и формы сигнала путем ограничения и т. д.

К таким устройствам можно отнести интегрирующую и дифференцирующую цепи, которые находят широкое применение в вычислительной технике, в системах развертки телевизионных приемников и в других случаях, когда необходимо ослабить высокочастотных составляющие импульсов.

Практически интегрирующую цепь (рис. 3.24, а .) можно рассматривать как фильтр нижних частот. При воздействии синусоидальных сигналов интегрирующая цепь сильнее ослабляет сигналы более высоких частот (и вносит некоторый фазовый сдвиг). В случае импульсных или прямоугольных сигналов их форма изменяется благодаря фильтрации высокочастотных сигналов.

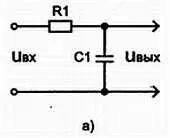
Рис. 3.24, а) Cxeма интегрирующей цепи

В практических схемах интегрирующих цепей постоянная времени t= RCвелика по сравнению с длительностью воздействующего импульса. В этом случае при ращение напряжения е сна конденсаторе мало по сравнению с напряжением е , приложенным к интегрирующей цепи. Тогда можно записать приближенное равенство:

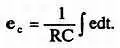
Таким образом, выходное напряжение интегрирующей цепи пропорционально интегралу входного тока e / R . Это можно объяснить, если обратиться к рис. 3.24, б и в .

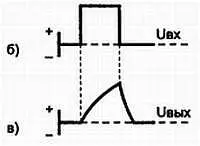
Рис. 3.24, б) форма входного импульса интегрирующей цепи, в) выходного импульса интегрирующей цепи

При подаче на вход схемы положительного импульса крутой фронт импульса действует на интегратор в течение очень короткого промежутка времени. Затем в течение времени, равного длительности импульса, действует напряжение, соответствующее плоской вершине импульса. Напряжение на конденсаторе нарастает по экспоненциальному закону. За время, равное постоянной времени цепи τ , напряжение на конденсаторе достигнет примерно 65 % максимального значения, а полностью конденсатор зарядится примерно в течение пяти постоянных времени (5 τ ). Так как постоянная времени интегрирующей цепи велика по сравнению с длительностью импульса, напряжение на конденсаторе не достигает максимального значения, а постепенно нарастает до некоторой величины (рис. 3.24, в ).

По окончании действия входного импульса конденсатор начнет разряжаться через резистор R1 и входную цепь. Разряд протекает медленно по сравнению со спадом входного импульса, и в результате на выходе формируется импульс, форма которого показана на рис. 3.24, в .

Если импульсы на входе интегратора имеют длительность, превышающую интервалы между ними (рис. 3.24, г ), то напряжение на конденсаторе будет постепенно нарастать.

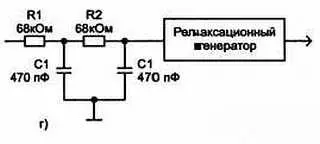
Рис. 3.24, г) длительность входных импульсов превышает интервал между ними

Такую схему можно использовать в качестве делителя частоты, так как уровень запуска релаксационного генератора будет достигаться только после определенного числа импульсов, поданных на вход. Постоянная времени этой цепи равна:

τ ~= R1( C1+ С2) + R2C2.

Интегрирующую цепь можно также построить, располагая катушкой индуктивности и резистором. Для этого в схеме на рис. 3.24, а резистор R1 следует заменить катушкой индуктивности, а конденсатор С1 — резистором. Однако, поскольку катушка индуктивности имеет еще и активное сопротивление, схема с резистором и конденсатором более широко применяется на практике.

В дифференцирующей цепи (рис. 3.25, а ) постоянная времени должна быть малой по сравнению с длительностью импульсов.

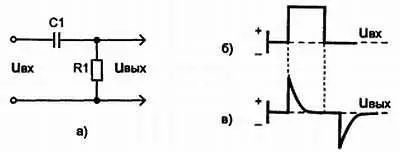
Рис. 3.25. а) Схема дифференцирующей цепи б)форма импульса на входе дифференцирующей цепи в)выходе дифференцирующей цепи

Эту цепь применяют в тех случаях, когда импульсы сравнительно большой длительности необходимо преобразовать в короткие импульсы с крутым фронтом. Цепь сохраняет крутой фронт импульса в той же полярности и по существу ведет себя как фильтр верхних частот, ослабляющий низкочастотные и пропускающий высокочастотные составляющие импульса.

При малой постоянной времени сопротивление резистора оказывается значительно больше реактивного сопротивления конденсатора. Поэтому выходное напряжение, равное падению напряжения на резисторе, приближенно выражается формулой:

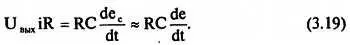
На рис. 3.25, б и в показаны соответственно формы импульса на входе и выходе дифференцирующей цепи. От начального момента действия импульса и в течение всей его длительности к входу схемы прикладывается постоянное напряжение. Если при подаче входного импульса конденсатор С1 не был заряжен, то в первый момент через конденсатор, а также через резистор R1 будет протекать большой ток. Таким образом, на резисторе сразу же появляется большое падение напряжения, благодаря чему на выходе очень быстро нарастает фронт импульса (рис. 3.25, в ). По мере заряда конденсатора протекающий через него ток уменьшается со скоростью, зависящей от постоянной времени цепи. При малой постоянной времени конденсатор быстро заряжается и ток перестает протекать по цепи. Таким образом, когда конденсатор полностью заряжен, напряжение на резисторе R1 спадает до нулевого уровня. В момент окончания действия импульса входное напряжение уменьшается до нуля, и конденсатор начинает разряжаться.