В Бессонов - Радиоэлектроника для начинающих (и не только)

Мощность переменного тока будет равна: Р= I∙ Ucos φ . При φ = π /2 мощность Р = 0. Это значит, что конденсатор является реактивным элементом и не потребляет электрической энергии.

Если вы возьмете три конденсатора емкостью 1 мкФ каждый, соедините их параллельно, подключите в сеть 220 В и будете наблюдать за счетчиком электрической энергии, который имеется в вашей квартире, то счетчик никак не отреагирует на это подключение, хотя они по мощности эквивалентны лампочке мощностью 48 Вт. Почему счетчик не реагирует? Потому что конденсатор (как и катушка индуктивности) обладает замечательным свойством: в положительный полупериод напряжения сети он заряжается и накапливает электрическую энергию, а в отрицательный полупериод напряжения сети он отдает эту энергию снова в сеть. Это как морской прилив и отлив: то вода пригоняет к берегу все, что на ней плавает, то все смывает с берега, унося в море. Имейте в виду, что конденсатор должен быть рассчитан на напряжение 250…300 В.

Из графика на рис. 3.16 видно, что реактивное (емкостное) сопротивление конденсатора уменьшается как с увеличением емкости, так и с увеличением частоты питающего переменного напряжения; этот график построен по формуле (3.11). Аналогичными свойствами реактивного элемента обладает и катушка индуктивности.

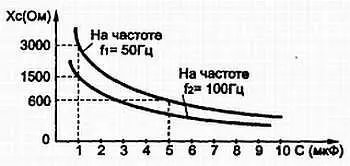
Рис. 3.16. Сопротивление конденсатора уменьшается как с увеличением ёмкости, так и с увеличением частоты

Внешний вид, УГО и БЦО катушки индуктивности приведены на рис. 3.17.

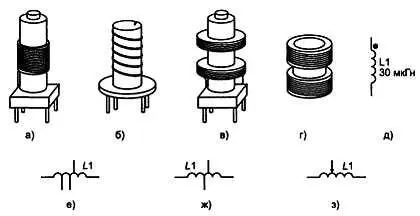
Рис. 3.17. Внешний вид, УГО и БЦО катушки индуктивности

Чтобы лучше понять свойства катушки индуктивности, проведем несколько экспериментов.

3.2.5. Катушка индуктивности обладает индуктивным сопротивлением, которое также называется реактивным

В качестве катушки индуктивности можно использовать первичную обмотку сетевого трансформатора. При последовательном включении катушки индуктивности и лампы накаливания к источнику постоянного тока лампочка горит ярко, а при включении к источнику переменного тока (в сеть частотой 50 Гц) — тускло либо вообще не горит. Почему? Потому что катушка индуктивности обладает индуктивным сопротивлением X Lчасть напряжения источника переменного тока гасится на катушке индуктивности, а постоянному току катушка оказывает малое активное сопротивление (сопротивление провода), которое можно вычислить по формуле:

R= ρ∙ L/ S

Индуктивное сопротивление катушки индуктивности определяется по формуле:

X L= 2π fL= 6,28∙ f (Гц)∙ L (Гн ). (3.13)

Здесь L — индуктивность катушки, измеряется в генри (Гн), миллигенри (мГн), микрогенри (мкГн).

1 Гн = 1000 мГн = 1 000 000 мкГн.

Конструктивные данные катушек индуктивности даны в описаниях устройств, рекомендованных к самостоятельному изготовлению.

Тогда закон Ома запишется так:

I m = U m/ X L= U m/2π fL= U m/ω L. (3.14)

3.2.6. Последовательное и параллельное соединение катушек индуктивности

Рис. 3.18. Последовательное соединение двух катушек индуктивности

Рис. 3.19. Параллельное соединение двух катушек индуктивности

Рис. 3.20. Последовательное соединение трёх катушек индуктивности

Рис. 3.21. Параллельное соединение трех катушек индуктивности

Формулы для вычисления общей индуктивности при последовательном и параллельном включении похожи на аналогичные формулы для вычисления общего сопротивления резисторов.

Если при изготовлении какого-либо прибора у вас не оказалось нужной индуктивности, но имеется большое количество катушек индуктивности других номиналов, их можно соединить последовательно или параллельно для получения нужного номинала. При последовательном соединении вычисления довольно простые, а вот при параллельном соединении необходимо затратить время на вычисления. Тоже самое приходится делать при последовательном соединении конденсаторов и при параллельном соединении резисторов. Для облегчения подбора второго элемента на рис. 2.22 ( глава 2 ) приведена номограмма.

3.2.7. Катушка индуктивности как накопитель магнитной энергии

В этом эксперименте в качестве катушки индуктивности можно использовать первичную обмотку сетевого трансформатора. При замыкании выключателя SA лампочка еле светится, а при размыкании выключателя SA она ярко вспыхивает. Это объясняется тем, что в момент включения элемента G часть энергии источника тратилась на создание магнитного толя катушки индуктивности, а при размыкании выключателя магнитное поле катушки индуктивности исчезает и запасенная в ней энергия отдается лампочке. Это явление называется самоиндукцией. Э.д. с самоиндукции препятствует увеличению тока при подключении источника питания к катушке индуктивности, а при отключении источника питания э.д.с. самоиндукции препятствует уменьшению тока в катушке. Здесь имеется ввиду, что все элементы включены последовательно.

3.2.8. Сила тока отстает от напряжения на катушке индуктивности на угол π /2

Так как i= I mSin ωt , a u= U mSin ( ωt — π /2), то, следовательно, напряжение на катушке индуктивности опережает силу тока по фазе на угол π/2 . Это видно также на векторный (рис. 3.22, а ) и на временной (рис. 3.22, б ) диаграммах.

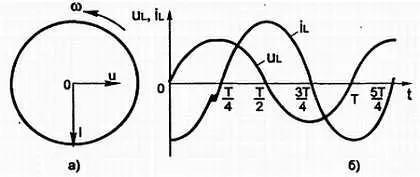
Рис. 3.22. Напряжение на катушке индуктивности опережает силу тока по фазе на угол 90°.

3.2.9. На активном сопротивлении (на резисторе) сила тока и напряжение совпадают по фазе

Так как i= I mSin ωt , и u= U mSin ωt , то, следовательно, напряжение на резисторе совпадает по фазе с силой тока . Это видно также на векторной (рис. 3.23, а ) и на временной (рис. 3.23, б ) диаграммах.