Эрл Гейтс - Введение в электронику

Счет в двоичной системе начинается с чисел 0 и 1. Как и в десятичной системе счисления, каждая двоичная цифра отличается от предыдущей на единицу. Сумма единицы и нуля дает единицу, а сумма двух единиц дает нуль, и при этом прибавляется единица в старшем разряде. На рис. 31-1 показана последовательность двоичных чисел, образованная по описанному алгоритму.

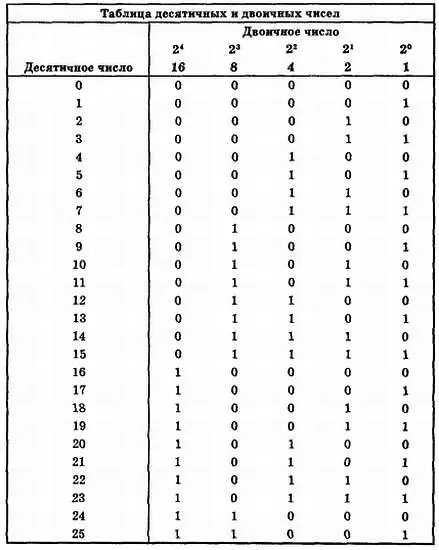
Рис. 31-1. Десятичные числа и эквивалентные двоичные числа.

Для определения наибольшего значения, которое может быть представлено данным количеством разрядов с основанием 2, используйте следующую формулу:

Наибольшее число = 2 n — 1,

где n— число битов (или число использованных значений разрядов).

ПРИМЕР:два бита могут быть использованы для счета от 0 до 3, так как

2 n- 1 = 2 2- 1 = 4–1 = 3.

Четыре бита необходимы для счета от 0 до 15, так как

2 n— 1 = 2 4— 1 = 16 — 1 = 15.

31-1. Вопросы

1. В чем преимущество двоичной системы счисления перед десятичной при использовании в цифровых цепях?

2. Как определить наибольшее значение двоичного числа при заданном числе разрядов?

3. Каково наибольшее значение двоичного числа с:

а. 4 битами,

б. 8 битами,

в. 12 битами,

г. 16 битами.

Как установлено, двоичное число представляет собой число с весом каждого разряда. Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда. Метод вычисления двоичного числа показан на следующем примере:

ПРИМЕР:

Число 45 является десятичным эквивалентом двоичного числа 101101.

Дробные числа также могут быть представлены в двоичной форме путем размещения двоичных цифр справа от двоичной запятой, так же как и десятичные цифры размещаются справа от десятичной запятой. Все цифры справа от запятой имеют вес, представленный отрицательными степенями 2 или дробными значениями разрядов.

Степень 2 ∙ Значение разряда

2 5= 32

2 4= 16

2 3= 8

2 2= 4

2 1 = 2

2 0= 1

десятичная запятая

2 -1= 1/2 1= 1/2 = 0,5

2 -2= 1/2 2= 1/4 = 0,25

2 -3= 1/2 3= 1/8 = 0,125

2 -4= 1/2 4= 1/16 = 0,0625

ПРИМЕР: Определить десятичное значение двоичного числа111011,011.

При работе с цифровым оборудованием часто бывает необходимо преобразовывать числа из двоичной системы в десятичную, и наоборот. Наиболее популярный способ преобразования десятичных чисел в двоичные — это последовательное деление десятичного числа на 2, с записью остатка после каждого деления. Остатки, взятые в обратном порядке, образуют двоичное число.

ПРИМЕР: Преобразовать11 в двоичное число последовательным делением на2 . (Самый Младший Разряд).

(1/2 = 0 означает, что 1 не делится на 2, так что 1 является остатком). Десятичное число 11 равно 1011 в двоичной системе.

Этот процесс может быть упрощен путем записи чисел упорядоченным образом, как это показано на примере преобразования 25 в двоичное число.

ПРИМЕР:

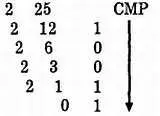
Десятичное число 25 равно двоичному числу 11001. Дробные числа преобразовываются по другому: число умножается на 2 и целая часть записывается как двоичная дробь.

ПРИМЕР: Преобразовать десятичную дробь0,85 в двоичную дробь последовательным умножением на2.

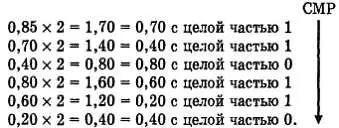
Умножение на 2 продолжается до тех пор, пока не будет достигнута необходимая точность. Десятичная дробь 0,85 равна 0,110110 в двоичной форме.

ПРИМЕР: Преобразовать десятичное число20,65 в двоичное число. Разделите20,65 на целую часть20 и дробную0,65 и примените описанные выше методы.

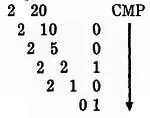
Десятичное 20 — двоичному 10100

и

Комбинируя два числа, получим20,65 10= 10100,1010011 2.

Это 12-разрядное число является приближенным, потому что преобразование дроби было прервано после получения 7 разрядов.

31-2. Вопросы

1. Чему равно значение каждого разряда 8-разрядного двоичного числа?

2. Чему равно значение каждого разряда для 8 разрядов правее десятичной точки?

3. Преобразуйте следующие двоичные числа в десятичные:

а. 1001;

б. 11101111;

в. 11000010;

г. 10101010,1101;

д. 10110111,0001.

4. В чем состоит процесс преобразования десятичных чисел в двоичные?

5. Преобразуйте следующие десятичные числа в двоичные:

а. 27;

б. 34,6;

в. 346;

г. 321,456;

д. 7465.

Код 8421 — это двоично-десятичный код (ДДК), состоящий из четырех двоичных разрядов. Он используется для представления цифр от 0 до 9. Обозначение 8421 относится к двоичному весу 4 разрядов.

Степени 2: 2 32 22 12 0

Двоичный вес: 8 4 2 1

Основным достоинством этого кода является то, что он допускает легкое преобразование из десятичной формы в двоичную, и наоборот. Поэтому двоично-десятичный код используется всегда, если не оговорено другое.

Каждая десятичная цифра (от 0 до 9) представляется двоичной комбинацией следующим образом:

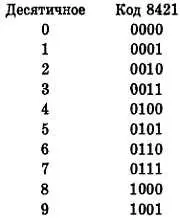
Хотя с помощью четырех двоичных разрядов можно представить 16 чисел (2 4), шесть кодовых комбинаций для чисел, больших 9 (1010,1011,1100, 1101, 1110 и 1111), в коде 8421 не используются.

Для того чтобы выразить любое десятичное число с помощью кода 8421, замените каждую десятичную цифру соответствующим 4-разрядным кодом.

ПРИМЕР: Преобразовать следующие десятичные числа в двоично-десятичный код:5, 13, 124, 576, 8769.

Для преобразования числа из двоично-десятичного кода в десятичную систему, разбейте число на группы по 4 разряда. После этого запишите десятичные цифры, соответствующие каждой 4-разрядной группе.