Эрл Гейтс - Введение в электронику

ПРИМЕР: Преобразуйте числа, записанные двоично-десятичным кодом в десятичную систему : 10010101, 1001000, 1100111, 1001100101001, 1001100001110110.

Замечание:Если в крайней группе слева не хватает разрядов до четырех, то к ней добавляются нули.

31-3. Вопросы

1. Что такое код 8421 и как он используется?

2. Преобразуйте следующие десятичные числа в двоично-десятичный код:

а. 17;

б. 100;

в. 256;

г. 778;

д. 8573.

3. Преобразуйте следующие двоично-десятичные коды в десятичные числа:

а. 1000 0010;

б. 0111 0000 0101;

в. 1001 0001 0011 0100;

г. 0001 0000 0000 0000;

д. 0100 0110 1000 1001.

РЕЗЮМЕ

• Двоичная система счисления — это простейшая система счисления.

• Двоичная система счисления содержит две цифры — 0 и 1.

• Двоичная система счисления используется для представления данных в цифровых и компьютерных системах.

• Двоичные данные представляются двоичными разрядами, которые называются битами.

• Термин бит происходит от названия двоичный разряд (binary digit)

• Значение каждого более высокого разряда двоичного числа увеличивается как степень 2.

• Наибольшее число, которое может быть представлено данным количеством разрядов в двоичной системе равно 2 n — 1, где n — количество разрядов.

• Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда.

• Дробные числа представляются отрицательными степенями 2.

• Для преобразования десятичного числа в двоичное, десятичное число последовательно делится на 2, и после каждого деления записывается остаток. Эти остатки, расположенные в обратном порядке, образуют двоичное число.

• Код 8421 или двоично-десятичный код используется для представления цифр от 0 до 9.

• Достоинством двоично-десятичного кода является возможность легкого преобразования чисел из десятичной формы в двоичную и наоборот.

Глава 31. САМОПРОВЕРКА

1. Запишите в двоичной форме десятичные числа от 0 до 27.

2. Сколько двоичных разрядов нужно для представления десятичного числа 100?

3. Опишите процесс преобразования десятичного числа в двоичное число.

4. Преобразуйте следующие двоичные числа в десятичные:

а. 100101,001011;

б. 111101110,11101110;

в. 10000001,00000101.

5. Опишите процесс преобразования десятичных чисел в двоично-десятичный код.

6. Преобразуйте следующие двоично-десятичные коды в десятичные числа:

а. 0100 0001 0000 0110;

б. 1001 0010 0100 0011;

в. 0101 0110 0111 1000.

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Перечислить и объяснить функции основных логических элементов.

• Нарисовать схематические обозначения для основных логических элементов.

• Начертить таблицы истинности для основных логических элементов.

Все цифровое оборудование, от простого до сложного, сконструировано с использованием небольшого количества основных схем. Эти схемы, называемые логическими элементами , выполняют некоторые логические функции с двоичными данными.

Существуют два основных типа логических схем: схемы принятия решений и память. Логические схемы принятия решений контролируют двоичные сигналы на входах и выдают выходной сигнал, основанный на состояниях входов и характеристиках логической схемы.

Схемы памяти используются для хранения двоичных данных.

Элемент И — это логическая схема, имеющая два или более входа и один выход. На выходе элемента И появляется 1 только тогда, когда на все его входы поступает сигнал 1. Если на какой-либо из входов поступает 0, на выходе появляется 0.

На рис. 32-1 показаны стандартные обозначения, используемые для элементов И. Элемент И может иметь любое количество входов, большее одного.

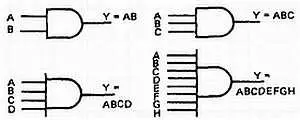
Рис. 32-1. Логические обозначения элемента И.

Показанные на рисунке обозначения представляют наиболее часто используемые элементы с двумя, тремя, четырьмя и восемью входами.

Работу элемента И отражает таблица на рис. 32-2. Такая таблица, называемая таблицей истинности, показывает выходное состояние элемента для любых возможных состояний входов.

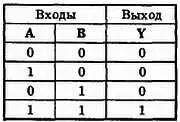
Рис. 32-2. Таблица истинности для двухвходового элемента И.

Входы обозначены А и В . Выход обозначен Y . Общее число возможных комбинаций в таблице истинности определяется следующей формулой:

N= 2 n ,

где N — общее количество возможных комбинаций, n — общее число входных переменных.

ПРИМЕР:

Для двух входных переменных N = 2 2= 4.

Для трех входных переменных N = 2 3= 8.

Для четырех входных переменных N = 2 4= 16.

Для восьми входных переменных N = 2 8= 256.

Элемент И выполняет операцию логического умножения. Логическое умножение известно как функция И.

Выход элемента И математически может быть представлен равенством Y = А ^ В или Y = АВ . Функция И — точка между двумя переменными А и В .

32-1. Вопросы

1. При каких условиях на выходе элемента И появляется 1?

2. Нарисуйте схематическое обозначение, используемое для элемента И с двумя входами.

3. Изобразите таблицу истинности для элемента И с тремя входами.

4. Какую логическую операцию выполняет элемент И?

5. Как алгебраически изображается операция, выполняемая элементом И?

На выходе элемента ИЛИпоявляется 1, если на любой из его входов подана 1. На его выходе появляется 0, если на все его входы поданы 0. Значения на выходе элемента ИЛИ с двумя входами приведены в таблице истинности на рис. 32-3.

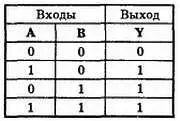
Рис. 32-3. Таблица истинности для двухвходового элемента ИЛИ.

Общее число возможных комбинаций выражается формулой N = 2 2= 4. В таблице истинности приведены все четыре комбинации.

Элемент ИЛИ выполняет логическую операцию сложения. Алгебраически операция, выполняемая элементом ИЛИ, выражается следующим образом Y = А + В или Y = А V В . Знак плюс обозначает функцию ИЛИ.

На рис. 32-4 изображены логические обозначения для элемента ИЛИ. Входы обозначены А и В, а выход обозначен Y. Элемент ИЛИ может иметь любое число входов, большее одного. На рисунке изображены элементы ИЛИ с двумя, тремя, четырьмя и восемью входами.