Эрл Гейтс - Введение в электронику
- Название:Введение в электронику
- Автор:
- Жанр:
- Издательство:Феникс
- Год:1998
- Город:Ростов-на-Дону
- ISBN:5-222-00417-1
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эрл Гейтс - Введение в электронику краткое содержание
Введение в электронику - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
4. Логически сложите слагаемые (объедините с помощью операции ИЛИ) от каждой петли, одно слагаемое на каждую петлю. (Каждое слагаемое извлекается из диаграммы Вейча и логически суммируется с другими, например ABC + BCD .)
5. Запишите упрощенное выражение.
ПРИМЕР: Упростите АВ + А -В + АВ -.
Шаг 1.Нарисуем диаграмму Вейча. Мы имеем две переменных А и В , поэтому используем таблицу для двух переменных.
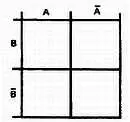
Шаг 2.Нанесем логические функции, помечая их знаком X в соответствующем квадрате.

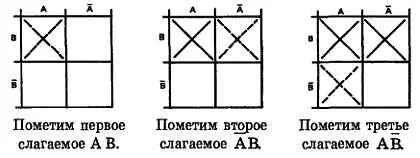
Шаг 3.Объединим соседние квадраты, помеченные знаком X , в наибольшие возможные группы. Проанализируем диаграмму — какая возможна наибольшая группа? Наибольшая возможная группа состоит из двух квадратов.
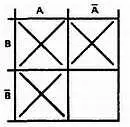
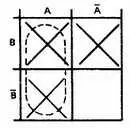
Одна из возможных групп показана штриховой линией.
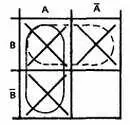
Другая возможная группа на этой диаграмме показана штриховой линией.
Шаг 4.Логически сложим эти группы (операция ИЛИ):
или А , или В = А + В.
Шаг 5.Упрощенным выражением для АВ + А - В + АВ -= Y является А + В = Y , что получено из диаграммы Вейча.
ПРИМЕР: Найдите упрощенное выражение для
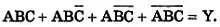
Шаг 1.Нарисуем диаграмму Вейча для трех переменных.
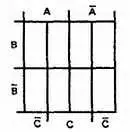
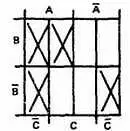
Шаг 2.Пометим знаком X логические функции каждого слагаемого на диаграмме Вейча.
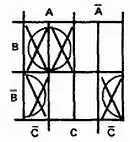
Шаг 3.Объединим соседние квадраты в наибольшие возможные группы.
Шаг 4.Запишем слагаемые для каждой петли, одно слагаемое на каждую петлю: AB, B -C -
Шаг 5.Упрощенным выраженном является АВ + ВС -= Y .
Отметим необычное объединение двух нижних квадратов. Четыре угла диаграммы Вейча считаются связанными, как если бы диаграмма была свернута в шар.
ПРИМЕР: Найдите упрощенное выражение для:
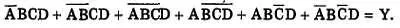
Шаг 1.Нарисуем диаграмму Вейча для трех переменных.

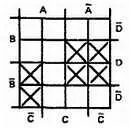
Шаг 2.Пометим знаком X логические функции каждого слагаемого на диаграмме Вейча.
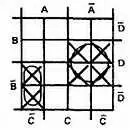
Шаг 3.Объединим соседние квадраты в наибольшие возможные группы.
Шаг 4.Запишем слагаемые для каждой петли, одно слагаемое на каждую петлю: A - D, AB - C -.
Шаг 5.Для получения упрощенного_выражения логически сложим полученные слагаемые: A - D + AB - C -= Y .
33-1. Вопросы
1. Какова функция диаграмм Вейча?
2. Сколько переменных может быть представлено на диаграмме Вейча?
3. Перечислите шаги при использовании диаграммы Вейча.
4. Упростите следующие выражения с помощью диаграмм Вейча.
а. AB - C + A - B - C + ABC -+ AB - C -+ A - B - C -= Y.
б. ABCD + AB - C - D + A - BCD -+ A - B - C-D + AB - C - D + A - B - CD + ABC - D -= Y .
в. AB -+ A -BD + B - C - D + B - C -+ A - BC - D = Y.
РЕЗЮМЕ
• Диаграммы Вейча обеспечивают быстрый и легкий метод приведения сложных логических выражений к их простейшей форме.
• Диаграммы Вейча могут быть составлены для двух, трех или четырех переменных.
• Упрощенные логические выражения получаются из диаграмм Вейча путем объединения помеченных знаком X квадратов в группы из двух, четырех или восьми квадратов и последующего логического сложения объединенных выражений.
Глава 33. САМОПРОВЕРКА
1. Опишите процедуру использования диаграммы Вейча для упрощения логических выражений.
2. Упростите следующее Булево выражение с помощью диаграммы Вейча:
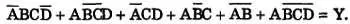
Глава 34. Последовательные логические цепи
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать функции триггера.
• Перечислить основные типы триггеров.
• Нарисовать схематические обозначения триггеров.
• Описать, как триггеры используются в цифровых цепях.
• Описать, как работает счетчик и сдвиговый регистр.
• Перечислить различные типы счетчиков и сдвиговых регистров.
• Нарисовать схематические обозначения счетчиков и сдвиговых регистров.
• Перечислить применения счетчиков и сдвиговых регистров.
Последовательные логические цепи состоят из цепей, требующих синхронизации и устройств памяти. Основным строительным блоком для последовательных логических цепей являются триггеры. Триггеры могут быть соединены вместе и образовывать счетчики, сдвиговые регистры и устройства памяти.
Триггеры принадлежат к категории цифровых цепей, которые называются мультивибраторами. Мультивибратор — это цепь с положительной обратной связью, имеющая два активных устройства, рассчитанных таким образом, что одно устройство проводит ток, в то время как другое устройство закрыто. Мультивибраторы могут хранить двоичные числа, импульсы счета, синхронизировать арифметические операции и выполнять другие полезные функции в цифровых системах.
Читать дальшеИнтервал:
Закладка:









