Борис Крук - ...И мир загадочный за занавесом цифр. Цифровая связь

0 + 0 = 0, 0 + 1 = 1, 1 + 1 =(10) 2

а вся таблица умножения сводится к четырем простейшим произведениям:

0 x 0 = 0, 1 x 0 = 0, 0 x 1 = 0, 1 x 1 = 1.

Не зря древние египтяне почти 4000 лет назад применяли двоичное умножение для своих громоздких иероглифических чисел!

Давайте воспроизведем снова задачу на умножение чисел 12x12 из математического папируса Ринда, записывая теперь уже числа не иероглифами, а в двоичной системе счисления. Число 12 имеет двоичную запись 1100. Напомним, что египтяне удваивали первый сомножитель (число 12) до тех пор, пока из комбинации степеней двойки не получался второй сомножитель (в нашем случае тоже число 12). Результат умножения они вычисляли путем суммирования определенных строк с записями удваиваемого сомножителя.

Занесем в таблицу результаты многократного удвоения числа 12 и соответствующие им степени двойки. А чтобы можно было легко разобраться с двоичными числами, приведем "веса" всех используемых разрядов:

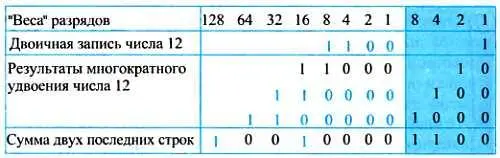
В правом столбце второй сомножитель получается при суммировании двух последних строк (это видно из анализа "весов" единичных разрядов, входящих в сумму). Значит, результат следует получить, суммируя (с учетом переноса единицы в старшие разряды) две последние строки левого столбца. "Веса" единичных разрядов этой суммы показывают, что произведение чисел равно 144.

И снова неожиданность, да еще какая: мы выполнили умножение, ничего не умножая, а только суммируя! Так поступают и современные компьютеры: они анализируют "веса" единичных разрядов одного из сомножителей и "узнают", какие строки, полученные последовательным удвоением другого сомножителя, нужно складывать. Заметим, что операция удвоения числа в вычислительной машине самая простая из всех операций: она заключается, как видно из таблицы, в сдвиге записи двоичного числа влево на одну позицию.

Итак, у десятичных цифр появился серьезный конкурент - двоичные цифры 0 и 1, которыми "предпочитают пользоваться" компьютеры. Да и не только они!

Еще 15 лет назад на Международной выставке роботов в Японии посетители могли увидеть изящного робота-музы канта, напоминающего средневекового рыцаря, закованного в латы, который с помощью электронного глаза читал ноты и переворачивал рукой нотные страницы. Его пальцы могли нажимать на клавиши электронного органа до 50 раз в секунду. Он мог исполнять любое произведение - от Баха до музыки битлзов.

"Начинку" робота составляли главный компьютер и 50 управляемых им микрокомпьютеров, ведающих всеми суставами и пальцами. Но ведь любой компьютер - и микроминиатюрный, занимающий всего один кристалл, и гигантский, размещаемый в большом зале, - оперирует только с двоичными цифрами. Значит, и интеллектуальные роботы (а среди них и шахматисты, и штангисты, и няньки для детей, и даже актеры) "предпочитают" пользоваться двоичными цифрами.

Но, что самое удивительное, робот-музыкант, "зная" только цифры 0 и 1, способен читать нотную запись, понимать человеческую речь и отвечать осмысленными фразами. Как все это происходит? Какими "магическими" свойствами обладают цифры 0 и 1, позволяющие выразить и нотную запись, и человеческую речь, и звуки бессмертной музыки? Об этом и пойдет речь в следующих главах.

Это строки стихотворения "Бармаглот" из знакомой всем веселой детской книжки "Алиса в Зазеркалье". Если предложить разным людям "распознать", какую конкретную информацию несут в себе эти строки, то вариантов будет столько, сколько и людей, пытающихся их расшифровать. В них не заложено никакого смысла! Это знаменитые "Джабберуокки" (что-то вроде бессмыслицы) — математика и логика Льюиса Кэрролла.

А вот такая фраза:

аеефикцыге рмчии,

на первый взгляд кажется еще более бессмысленной, чем "Джабберуокки". Однако она как раз содержит в себе вполне определенную информацию. В этой записи мы зашифровали название первой части нашей книги "Магические цифры" путем перестановки в нем букв.

Правило перестановки может быть, конечно, любым. Однако, чтобы прочесть исходный текст, нужно сделать правило легко запоминаемым. Мы осуществили перестановку следующим образом. Сначала записали шифруемый текст в квадратную таблицу под ключевым словом "шифр":

Затем пронумеровали столбцы в соответствии с очередностью появления букв слова "шифр" в алфавите (например, буква "и" идет по алфавиту раньше буквы "р" и остальных букв слова "шифр", поэтому второму столбцу присвоен номер 1, четвертому — номер 2 и т. д.). И наконец, переписали буквы всех столбцов в соответствии с присвоенными номерами,т. е. сначала буквы столбца под номером 1, затем под номером 2 и т. д. Читатели из интереса могут придумать какой-нибудь другой способ шифровки.

Способы буквенного шифрования текстов (или еще говорят "кодирования") известны очень давно. Так, знаменитый в истории римский диктатор Гай Юлий Цезарь для тайной переписки со своими сторонниками среди римских политиков применял такой способ кодирования: сдвигал весь алфавит на определенное число букв влево или вправо. Если каждую букву текста "Магические цифры" заменить предшествующей буквой алфавита (при этом букве "а" предшествует буква "я"), то получится фраза

лявзцдризд хзупъ,

зашифрованная кодом Цезаря.

Однако чаще всего буквенные тексты шифруют с помощью цифр, т. е. цифровым кодом, что, возможно, связано со стремлением сделать сообщение недоступным для тех, кому оно не предназначено. Вот пример цифрового кодирования текста.

Попробуйте расшифровать следующую запись:

301 033 020 016 052 402 163 502 230 403.

Вы, наверное, уже догадались, что приведенным набором цифр представлена все та же фраза "Магические цифры". Цифровой ее код получен так. Буквы русского алфавита были расположены в прямоугольной таблице 4x8 произвольным образом:

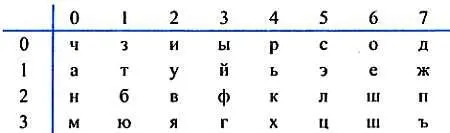
Затем каждая буква была заменена двумя цифрами: соответствующими номерами строки и столбца. Группирование же цифр по три в шифрованной записи было сделано лишь для того, чтобы сбить с толку дешифровальщика, т. е. вас, читатель.

На первый раз, думаем, это удалось.

В приведенном примере алфавит из 32 символов (букв) был заменен алфавитом из десяти символов (цифр). Такое положение справедливо и в общем случае: любой алфавит, состоящий из конечного числа каких-либо символов, можно заменить алфавитом из других символов, причем новых символов может быть существенно меньше.