Евгений Айсберг - Цветное телевидение?.. Это почти просто!

Это означает, что для воспроизведения эффекта, производимого излучением с длиной волны 500 нм, нужно прежде всего изменить его путем добавления некоторого количества первичного красного цвета. Тогда соответствующим образом дозированная смесь зеленого и синего создаст такое же ощущение, что и смесь излучения с длиной волны 500 нм с примесью красного цвета. Именно это количество красного со знаком минус должно вводиться в смесь трех первичных цветов.

На практике анализируемый световой луч оптическими методами разделяется на три части и, направляется на три фильтра, из которых один пропускает только красный, второй — только зеленый и третий — только синий цвета.

Интенсивность света замеряется, например, фотоэлементом. Для воспроизведения такого же окрашенного светового луча нужно соответствующим образом дозировать интенсивность трех белых фонарей, прикрытых идентичными описанными ранее цветными фильтрами, и наложить полученные цветные пятна друг на друга на белом экране.

Следовательно, можно сказать, что при трехцветном способе воспроизведения цветного изображения каждый цвет определяется тем, сколько в нем содержится красного, зеленого и синего, т. е. группой из трех чисел. Математики назвали бы эти три числа координатами и сказали бы, что цвета образуют трехмерное пространство.

Мы же радиотехники, а не математики, но мы весьма признательны последним за то, что они снабдили нас некоторым количеством рабочих инструментов, объединенных названием «методы расчета». На этот раз мы будем говорить как математики. И раз пространство цветов трехмерно, мы изобразим его в виде прямоугольного шестигранника (куба) и обозначим его оси OR, OG и ОВ (рис. 18).

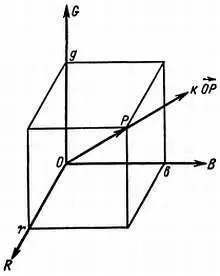
Рис. 18. Трехмерное изображение цвета.

Следовательно, некая точка Р на нашей пространственной фигуре характеризуется тремя координатами R, G и В . Предположим, что мы умножаем все три координаты на заданный коэффициент k. Тогда вектор ОР станет равным k · ОР , т. е. его модуль (так называют длину вектора) умножается на величину k , но его направление остается неизменным. На практике это означает, что интенсивность света увеличена в k раз без какого бы то ни было изменения его качественных характеристик.

Из этого становится понятно, что, если нужно будет разъединить эти два аспекта — интенсивность света и внутренне присущие ему качества, которые воспринимаются как яркость и цветовой тон с насыщенностью, можно найти более простые средства для их изображения.

Возьмите трехмерное изображение трехцветного способа воспроизведения цветов и исключите одно из измерений (например, яркость света), что же останется в итоге? Ровно столько, сколько требуется для изображения характеристик на одной плоскости, а рисунки на плоскости легче понимать, чем рисунки в пространстве.

Но мы исходим из пространства, характеризуемого тремя координатами R, G и В , а теперь мы говорим об изъятии одной из величин (яркости света), которая по своей природе включается в состав этих трех. Но, увлекаемые математическим задором, мы берем матрицы изменения координат, т. е. операторы или «математические существа», с которыми наш читатель, может быть, недостаточно знаком?

Сразу же отметим, что имеется множество способов изобразить характеристики цвета на плоскости, не прибегая к научным выкладкам.

Впервые в истории цветовой график на плоскости составил английский физик Максвелл, который известен составлением дифференциальных уравнений, характеризующих распространение электромагнитных волн. Треугольник Максвелла (рис. 19) представляет собой равносторонний треугольник, вершины которого соответственно характеризуют чистые цвета: красный, синий и зеленый, но при таком изображении совершенно не учитывается яркость света. Теоретически внутри этого треугольника должны размещаться все цветовые тона и все степени насыщенности, которые можно получить трехцветным способом воспроизведения цветных изображений.

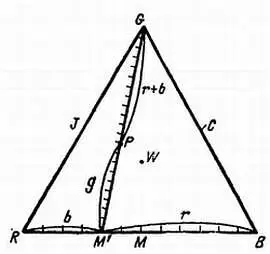
Рис. 19. Треугольник Максвелла .

Кроме вершин R, Gи Вобозначены следующие точки: М(пурпурный цвет — середина линии BR), С— (сине-зеленый цвет) — середина линии GB, J(желтый цвет) — середина линии RG; центр тяжести треугольника — точка Wсоответствует белому цвету. Предстоит найти точку P, соответствующую цвету, представляющему собой смесь трех основных цветов в следующем соотношении: R = 8, G= 9,5, В = 4.

Сначала находим барицентр М'для точек Ви R, для чего делим линию RBна 12 равных частей: RM'= 4, ВМ'= 8, затем для нахождения барицентра всей системы соединяем вершину Gс точкой М'и делим линию GМ' на 21,5 равных частей: РМ' = 9,5, GP= 12. Искомый цвет — желтый, находящийся на одинаковом расстоянии от насыщенного желтого и белого цветов.

Некая точка Р , расположенная внутри треугольника, представляет собой характеристику цвета. Определить, что представляет собой этот свет, можно следующим образом. Расположенные на стороне BR точки характеризуют цвета, содержащие основные синий и красный цвета, но не имеющие в своем составе зеленого. Например, расположенная на середине прямой BR точка М соответствует пурпурному , т. е. дополнительному к зеленому цвету; точно так же расположенная на середине прямой RG точка J соответствует желтому цвету (дополнительному к синему, который находится на противолежащей вершине); средняя на линии BG точка С характеризует сине-зеленый цвет (дополнительный к красному, находящемуся на противолежащей вершине). Центр тяжести треугольника соответствует цвету, состоящему из равных долей красного, синего и зеленого, т. е. белому цвету.

Чтобы найти на треугольнике точку, соответствующую заданному цвету, соотношение основных цветов в котором мы знаем, нужно представить, что треугольник физически состоит из трех идеальных (бесконечно жестких, но не имеющих никакой массы) планок, и в вершины треугольника поместить массы, пропорциональные величинам основных цветов: массу r в вершину R , массу g в вершину G и массу b в вершину В . Затем нужно найти центр тяжести полученной системы, который, естественно, не совпадает с геометрическим центром тяжести W треугольника (рис. 19). Найденную точку называют барицентром . Сначала сторону BR делят на равные части, количество которых равно b + r , и барицентр М' помещают на расстоянии r частей от вершины В (т. е. на расстоянии Ь частей от вершины R ); затем найденную точку соединяют с вершиной G линией GM' , которую делят на равные части, количество которых равно r + b + g ; точка Р , символизирующая искомый цвет, находится на расстоянии g частей от точки М' (т. е. на расстоянии b + r частей от вершины G ).