Юрий Ревич - Занимательная электроника

Итак, запись числа в двоичной системе требует всего двух цифр, начертание которых заимствовано из десятичной системы и выглядит, как 0 и 1. Число, например, 1101 тогда будет выглядеть так:

1·2 3+ 1·2 2+ 0·2 1+ 1·2 0= 13

Чтобы отличить запись числа в различных системах, часто внизу пишут основание системы:

1101 2= 13 10.

Если система не указана, то имеется в виду обычно десятичная, но не всегда — часто, когда из контекста понятно, что идет речь об электронных устройствах, не указывают не только основание два, но и под словом «разрядность» имеют в виду количество именно двоичных, а не десятичных разрядов (таков, скажем, смысл термина «24-разрядный цвет»).

Шестнадцатеричная система имеет, как ясно из ее названия, основание шестнадцать. Для того чтобы получить шестнадцать различных знаков, изобретать ничего нового не стали, а просто использовали те же цифры от 0 до 9 для первых десяти и заглавные латинские буквы от А до F для одиннадцатого-шестнадцатого знаков (часто вместо заглавных букв употребляют и строчные, с теми же значениями). Таким образом, известное нам число 13 10выразится в шестнадцатеричной системе, как просто D 16. Соответствие шестнадцатеричных знаков десятичным числам следует выучить наизусть: А — 10, В — 11, С — 12, D — 13, Е — 14, F — 15. Значения больших чисел вычисляются по обычной формуле, например:

A2FC 16= 10·16 3+ 2·16 2+ 15·16 1+ 12·16 0= 40960 + 512 + 240 + 12 = 41724 10.

Перевод из одной системы счисления в другую

Как следует из изложенного, перевод в десятичную систему любых форматов не представляет сложности и при надлежащей тренировке может осуществляться даже в уме. Для того чтобы быстро переводить в десятичную систему двоичные и шестнадцатеричные числа, следует выучить наизусть таблицу степеней двойки до 16 (табл. 14.3) и представления некоторых чисел в двоичной и шестнадцатеричной формах (табл. 14.4).

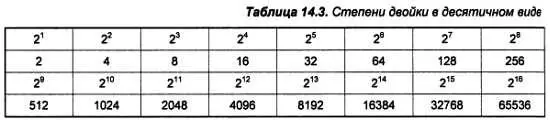
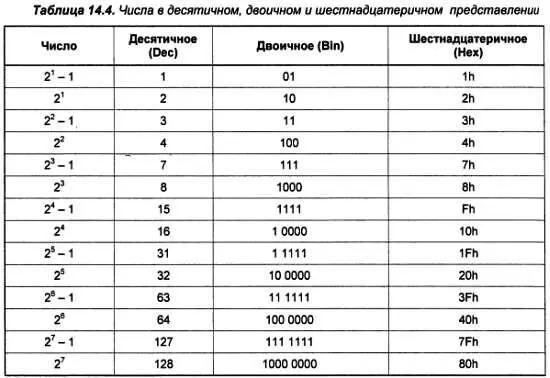
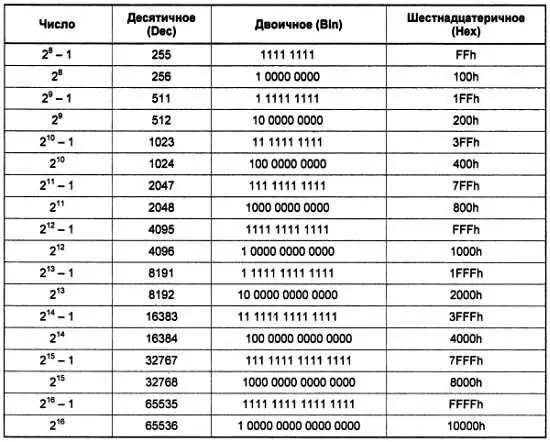
Буква h добавляется к шестнадцатеричному представлению числа, чтобы отличить его от десятичного, не используя индекса 16 (в разных языках программирования есть и другие способы, см. далее). На первое время достаточно запомнить только маленькие числа, а для образования двоичных и шестнадцатеричных чисел понять принцип, остальное выучится позже само.

Из табл. 14.4 видно, что из двоичной в шестнадцатеричную системы и обратно переводить совсем просто. Двоичное число достаточно разбить на тетрады (т. е. группы из 4-х цифр) и перевести каждую в отдельности. Например, число 59 10, т. е. 0011 1011 2, будет равно 3Bh. Еще проще обратный перевод — каждое шестнадцатеричное число заменяется группой из 4-х двоичных цифр. Соответственно, число A2FC 16выразится так: 1010 0010 1111 1100 2. Заметьте, что пробелы между тетрадами в двоичных числах введены просто для удобства восприятия, подобно пробелам между тройками разрядов (классами) в записи больших десятичных чисел, и никакой иной нагрузки не несут. При записи двоичных чисел в тексте программ, как ассемблерных, так и программ на языках высокого уровня, естественно, эти пробелы ставить запрещается. Обычно при этом для удобства ведущие нули нередко не опускаются (хотя в табл. 14.4 они и опущены) — число 15 чаще всего записывается в виде 0Fh. Почему так удобнее, вы поймете далее.

* * *

Заметки на полях

Почему в табл. 14.4 приведены именно эти числа? Числа, на единицу меньшие степени двойки, имеют в электронике и в программировании большое значение. Если вы посмотрите в таблицу внимательно, то увидите, что наибольшее число с количеством разрядов, равным степени двойки, содержит единицы во всех разрядах, т. е. как раз и равно этой степени минус единица. При этом количество всех чисел с таким количеством разрядов равно степени двойки. Другими словами, память, содержащая ровно 256 (2 8) ячеек, будет иметь номер (адрес) последней ячейки, равный 255, или FFh. Наибольшее число, до которого может досчитать 8-разрядный двоичный счетчик, также равно FFh, поскольку если подать на него еще один импульс (257-й по счету), он обнулится, ибо 9-го разряда, где могла бы записаться старшая единица, у него не существует. Потому с такими числами приходится иметь дело очень часто, даже чаще, чем с собственно степенями двойки.

* * *

Сложнее переводить из десятичной системы, и для этого в учебниках рекомендуется устрашающая процедура, основанная на делении столбиком (см., например [17]). Я сейчас попробую вам показать модификацию этого способа, который позволяет переводить числа в двоичную систему несколько более простым методом, причем небольшие числа можно переводить даже в уме.

Для начала запомним, что разряды двоичного числа нумеруются с нуля — т. е., к примеру, разряд номер 3 окажется четвертым справа. Теперь пусть мы имеем, например, десятичное число 59. Подбираем наибольшую степень двойки из табл. 14.3, не превышающую этого числа: 32, что есть 5-я степень. Ставим 1 в 5-м разряде: 100000. Вычитаем подобранную степень из исходного числа (59–32 = 27) и подбираем для остатка также степень, его не превышающую: 16 (2 4). Ставим единицу в 4-м разряде: 110000. Повторяем процедуру вычитания-подбора: 27–16 = 11, степень равна 8 (2 3), ставим единицу в 3-м разряде: 111000. Еще раз: 11 — 8 = 3, степень равна 2 (2 1), так что 2-й разряд оказался пропущен, ставим в нем ноль, а единицу во 1-м разряде: 111010. Последнее вычитание дает 1, которую и ставим в младший (нулевой) разряд, окончательно получив 59 10= 111011 2.

Слово «байт» ( byte ) представляет собой сокращение от Binar Ydigi T Eight — «восемь двоичных цифр». Другими словами, байт — это просто восьмиразрядное двоичное число. Соответственно, он имеет ровно два шестнадцатеричных разряда, или две двоичных тетрады. Такой байт был введен фирмой IBM в конце 50-х годов прошлого века, до этого (а в СССР — и после этого, вплоть до 1969 года) применялись байты с другим количеством разрядов: 5, 6 и 7.

Почему именно 8 разрядов? Да просто потому, что так удобно — число кратно степени двойки, т. е. легко масштабируется. Скажем, шестнадцатиразрядное число — просто два байта, записанные подряд, подобно тетрадам в самом байте. В то же время число в 8 разрядов — относительно невелико и одновременно достаточно емко: имеет 256 значений, которых с лихвой хватает, к примеру, для представления всех печатных знаков европейских алфавитов. Поэтому в настоящее время байт — общепринятая единица измерения информации, т. к. основную единицу — бит — на практике применять неудобно из-за ее мелковатости, числа получаются слишком большими. Применяют и меньшие единицы: кроме бита, это полубайт, или тетрада — одно шестнадцатеричное число.