Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Если подобную операцию проделать с десятичным числом, т. е. сместить все цифры на один знак влево и справа приписать нуль, то исходное число увеличится в 10 раз. Но сейчас мы имеем дело с двоичным числом, и я не представляю, какой результат дает эта операция.

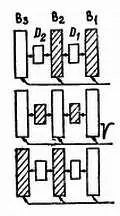
Л. — Но это очень просто — число умножается на 2. В этом заключается первая возможность нашей системы. Каждый посылаемый на провода Z импульс удваивает первоначально записанное число. Но наш сдвигающий регистр обладает еще более интересными возможностями. Посмотри, какие импульсы выдаст триггер В 3 после трех последовательных сбросов на нуль с помощью подачи импульсов на вход Z .

Н. — Чтобы мне было легче ориентироваться, я попробую разобраться на уже рассматривавшемся нами случае с первоначально записанным числом 011. Первый поданный на вход Z сигнал изменяет нашу запись на 110, но, как я полагаю, при этом мы должны учитывать и то обстоятельство, что триггер В 3 не даст импульса, ибо он переключается из положения 0 в положение 1.

Л. — В самом деле он дает только положительный импульс, который мы задерживаем с помощью диода. Следовательно, на выходе триггера В 3 ничего нет. А что произойдет при следующем сбросе на нуль?

Н. — О, теперь это ужасно сложно! Как я вижу, триггер В 2 , находящийся в положении 1, под воздействием импульса Z опрокинется в положение нуль. По-моему, он должен дать на выход импульс, потому что нас интересуют только импульсы, соответствующие переходу на нуль. Импульс с триггера В 2 поступает на элемент задержки D 2 , откуда он через некоторое время поступает на триггер В 3 и переключает его на 1 . Но я не очень хорошо представляю, что в итоге получилось.

Л. — В итоге мы получили импульс с триггера В 3 и записанное на регистре число превратилось в 100. При третьем переключении регистра на нуль мы вновь получим импульс с триггера В 3 , потому что он переходит на нуль из положения 1 . Теперь уже ни один триггер не может переключиться в положение 1, так как запись постепенно перемешалась и в результате полностью вышла за пределы регистра.

Н. — Но это более чем странно! Трехкратным переключением на нуль ты выталкивал цифру за цифрой записанное в регистре число. Только вытолкнул его не в том направлении, которое нам нужно; сначала мы получили отсутствие импульсов (цифра четверок), затем получили один импульс (цифра двоек) и, наконец, еще один импульс (цифра единиц).

Л. — Совершенно верно, мы цифру за цифрой вытолкнули наше число с того места, где оно было записано. Иначе говоря, на выходе S 3 мы получили наше число в последовательной форме. Ты правильно заметил, что выходящее из регистра число заканчивается единицами. При желании получить его единицами вперед, следует записать число на трех триггерах в обратном порядке: единицы подать на вход Е 3 , двойки — на вход Е 2 и четверки — на вход Е 1 .

Н. — Таким образом, мы можем сказать, что твой сдвигающий регистр способен преобразовывать параллельное представление числа в последовательное.

Л. — О, ты знаешь, транзисторы этой схемы способны (да позволят мне так сказать) не только на один фокус. Схема может выполнить и обратное преобразование. Представь себе, что мы подаем на вход А последовательное число и после передачи очередной цифры посылаем импульс сброса на нуль. Первая цифра записывается триггером B 1 , а затем импульс сброса на нуль продвигает ее на триггер В 2 . В этот момент следующая цифра записывается предварительно выставленным на нуль триггером B 1 .

Второй поступающий на вход Z импульс сброса на нуль продвигает первую цифру с триггера В 2 на триггер В 3 и вторую цифру с В 1 на В 2 . В это время триггер B 1 выставлен на нуль и готов получить третью цифру передаваемого на вход А числа в последовательной форме.

Н. — Действительно, очень умная схема, на этот раз она преобразовала последовательное представление числа в параллельное.

Л. — Но этим мы еще не исчерпали всех возможностей сдвигающего регистра. Представь себе, что на входы E 1,Е 2 и Е 3 нашей схемы мы подали параллельное число. А через некоторое время подаем еще одно такое же число на эти же входы: единицы на E 1 , двойки на Е 2 и четверки на Е 3 . Что мы получим в результате?

Н. — Ужасную смесь!

Л. — Совсем нет. Рассмотрим, что произойдет на одном из триггеров. Предположим, что после записи первого числа он стоит на нуле. Если в соответствующем этому триггеру месте второго числа стоит нуль, то триггер не получит никакого импульса и останется на нуле. Но при записи второго числа наш триггер может получить импульс (на соответствующем ему месте находится единица) и тогда он переключится на 1. Возможно также, что при записи первого числа триггер получит импульс, а при записи второго импульса не получит. В этом случае, как и в предыдущем после передачи второго числа, триггер будет стоять на 1. Как ты видишь, во всех этих трех случаях на каждом триггере мы получим цифру, равную сумме соответствующих цифр из двух чисел.

Н. — Очень занятно, но признайся, что все рассказанное тобой справедливо лишь для некоторых случаев.

Л. — Сейчас я докажу тебе, что справедливо для всех случаев. Предположим, например, что триггер В 1 при записи первого числа получил один импульс (что означает, что в первом числе на месте единиц стоит цифра 1). Теперь предположим, что при записи второго числа на вход Е 1 поступил еще один импульс. Этот импульс переключит триггер на нуль и тем самым запишет последнюю цифру суммы двух полученных цифр. При опрокидывании на нуль триггер посылает импульс на элемент задержки D 1 . Этот импульс представляет собой не что иное, как единицу, переносимую при сложении в следующий разряд. После того как сдвигающий регистр зафиксирует второе число, эта переносимая единица поступает на триггер В 2 и прибавляется к записанной в нем цифре, т. е. переключает триггер В 2 из одного состояния в другое.

Н. — Поразительно, твоя схема способна производить сложения и учитывать переносы единиц в следующие разряды. Это идеальное решение для создания сумматора.