Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

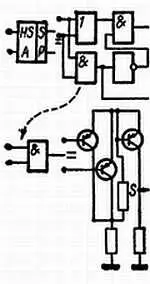
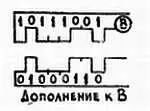
Л. — Не волнуйся, Незнайкин. Системы для выполнения арифметических вычислений всегда состоят из большого количества одинаковых и относительно простых устройств, которые в свою очередь распадаются на еще более простые узлы. Но как бы то ни было, сумматор, структурная схема которого изображена на рис. 131 и 132, способен мгновенно выдать сумму двух «параллельных» чисел, поданных одно за другим на его входы.

Н. — А если мы захотим сложить числа, представленные в последовательной форме?

Л. — В этом случае следует взять аналогичное устройство, используя только два элемента А , один элемент ИЛИ для выдачи переносимых в следующий разряд единиц и одну запоминающую схему, служащую для приема переносимых из предыдущего разряда единиц, например из разряда двоек в каскаде сложения четверок. Конструкция этого устройства относительно проста, но ее описание отвлекло бы нас от основной темы. Необходимо отметить, что последовательный сумматор состоит из меньшего количества деталей, но он обладает серьезным недостатком — необходимостью запоминать выходящее последовательное число. А в сумматоре, изображенном на рис. 131 и 132, ответ выдается незамедлительно (не требуется ждать, пока пройдут все цифры последовательного числа) и поступает на выход сразу же после подачи на входы слагаемых параллельных чисел.

Н. — Хорошо, теперь я более или менее умею складывать. Но скажи, пожалуйста, как производят вычитание?

Л. — Обычно проблему обходят. Предположи, что нам нужно из числа А вычесть число В . Для начала к А прибавляем одну единицу, а затем прибавляют противоположное В число (его также называют дополнением к В ) и при этом сложении не учитывают переноса.

Н. — Что ты называешь противоположным В числом?

Л. — Очень просто, это число, которое получается из числа В , если все его нули заменить единицами, а все его единицы нулями. Число В меньше А , и поэтому слева к нему нужно дописать несколько цифр. При преобразовании числа В в противоположное ему число все нули превращаются в единицы. Возьмем для большей наглядности числовой пример. Предположим, что А равно 101 101, (т. е. 45), а В равно 1011.

Н. — Иначе говоря, одиннадцати.

Л. — Браво, Незнайкин. Ты очень хорошо усвоил двоичную систему счисления. Следовательно, число В мы должны записать в следующем виде:

001 011,

чтобы оно, как и число А , состояло из шести знаков. В результате преобразования его в противоположное ему число получаем:

110 100.

А теперь позволь мне, Незнайкин, задать тебе один вопрос: что мы получим, если это противоположное число прибавим к числу В ?

Н. — Я думаю, что это сложение не представляет труда везде, где в одном из чисел стоит 1, в другом числе стоит нуль. Поэтому сумма этих двух чисел будет равна шестизначному числу, где все цифры 1, т. е. мы получим 111111.

Л. — Браво, совершенно верно! А теперь прибавь к полученному результату одну единицу.

Н. — Хорошо, если я прибавлю эту единицу, то сумма единиц даст нам нуль. Я переношу 1 в следующий разряд, прибавив ее к имеющейся здесь 1, я должен записать нуль на месте двоек и запомнить 1… Хм, очень любопытно, в итоге я получу 1000000.

Л. — Правильно. Но теперь в твоем числе семь знаков. Если пренебречь последним переносом, у нас останется лишь нуль. Как ты видишь, в результате сложения противоположного В числа и единицы даст нам нечто эквивалентное — В . Следовательно, для получения нужного результата мне достаточно прибавить это число к числу А . Операция имеет следующий вид:

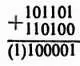
Н. — Я вижу, что в полученном результате слева стоит единица в скобках. Это несомненно появилось вследствие того, что ты не хочешь учитывать последний перенос.

Л. — Совершенно верно. Если теперь прибавить еще одну единицу, то в результате получим 100010. Преобразовав двоичное число в десятичное, получим 34, которое точно соответствует разности 45 и 11.

Н. — Должен признаться, что, не прибегая к двоичной системе счисления, я получил бы верный результат значительно быстрее!

Л. — Ты, может быть. Но электронные машины считают в двоичной системе счисления быстрее, чем в десятичной, даже если учитывать время, необходимое для преобразования.

Н. — Система автоматического счета положительно очень забавна. Не можешь ли ты объяснить мне, как производят умножение?

Л. — На этот раз ты проявляешь исключительную смелость. Схема устройства в самом деле довольно сложная.

Для начала я покажу тебе, как выглядит умножение двоичных чисел по правилам двоичной арифметики. Предположим, что нам нужно перемножить множимое 11010 (или 26) и множитель, равный 13…

Н. — Иначе говоря, 1101.

Л. — О! Ты действительно очень здорово преобразуешь десятичные числа в двоичные. Как ты видишь, наш множитель состоит из следующих слагаемых:

одна единица;

нуль двоек;

одна двойка в квадрате;

одна двойка в кубе.

Следовательно, для получения произведения, мы должны сложить следующие слагаемые:

единица, умноженная на множимое;

нуль, умноженный на это множимое, умноженное на два (иначе говоря, на множимое, к которому справа приписан нуль — 110100);

единица, умноженная на множимое, умноженное на четыре (иначе говоря на множимое, к которому справа приписали два нуля — 1101000);

единица, умноженная на множимое, умноженное на восемь (иначе говоря, на множимое, к которому справа приписали три дополнительных нуля — 11010000).

Следовательно, всю операцию умножения мы можем записать в следующем виде:

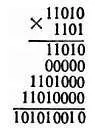
Н. — Теперь, когда я достаточно привык к двоичной системе счисления, твое умножение мне в точности напоминает операцию умножения, которую мне столько раз приходилось выполнять в десятичной системе счисления. Но больше всего меня смущает сложение частичных произведений. Я подозреваю, что выполнить эту операцию с помощью электронных схем окажется ужасно трудно.