И. Хабловски - Электроника в вопросах и ответах

Емкость диода меняется при изменениях обратного напряжения смещения диода. Начальное обратное напряжение подводится к диоду от делителя R 1R 3, шунтированного конденсатором C 1. Резистор R 2развязывает схему питания от резонансного контура генератора. Мгновенное значение напряжения на емкостном диоде является суммой напряжения смещения и напряжения низкой частоты, подведенного с помощью трансформатора. В результате к LC-контуру генератора параллельно подключается переменная емкость. Из-за того что приращение емкости ΔСемкостного диода изменяется вместе с изменением модулирующего сигнала, частота колебаний генератора подвергается изменению, пропорциональному амплитуде сигнала.

Помимо представленных методов непосредственной модуляции применяется метод косвенной частотной модуляции, позволяющий поддерживать соответствующее постоянство несущей частоты при отсутствии модуляции. Для осуществления такого метода используются модулятор Армстронга (косвенный частотный модулятор — прим. перев .), снабженный кварцевым генератором, и схемой фазовой модуляции, вырабатываемой путем суммирования сдвинутых на 90° боковых полос амплитудной модуляции с несущей. В результате использования схемы, позволяющей перейти от фазовой модуляции к частотной, и ограничения амплитуды выходного сигнала получают сигнал с чистой частотной модуляцией.

Большинство используемых частотных демодуляторов, служащих для получения модулирующего сигнала из частотно-модулированного, работает на принципе преобразования изменений частоты в изменения амплитуды и последующего детектирования сигнала с амплитудной модуляцией с применением обычных методов. Известны также частотные демодуляторы, работающие на принципе счета импульсов, а также более сложные демодуляторы, выполняемые в виде интегральных микросхем.

Характерным для техники частотной демодуляции является то, что собственно демодулятору, как правило, предшествует ограничитель амплитуды. Задачей ограничителя является исключение изменений сигнала, вызванных мешающими сигналами, для эффективного подавления на выходе демодулятора.

Простым ограничителем служит усилитель, управляемый сигналом, превышающим уровень максимального (без искажений) возбуждения транзистора между отсечкой и насыщением. Транзистор, работающий в схеме ограничителя, представлен на рис. 11.17, б и в .

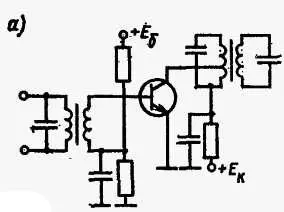
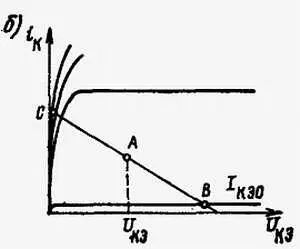
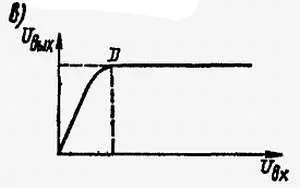
Рис. 11.17. Транзисторный ограничитель:

а— электрическая схема; б— рабочий диапазон на плоскости коллекторных характеристик; в— характеристика ограничения

В рабочей точке А ограничителя применяется относительно низкое напряжение, питающее коллектор. Если входной сигнал превышает пределы В и С , дальнейшее увеличение уровня выходного сигнала за этими пределами невозможно. Наименьший входной сигнал, который вызывает ограничительное действие ограничителя, называется порогом ограничении. Сигналы больше порогового, т. е. выше точки D , срезаются (ограничиваются) сверху и снизу. Резонансный контур, включенный в цепь коллектора, возвращает им синусоидальную форму.

Наиболее простым частотным детектором является детектор, работающий на скате амплитудной характеристики резонансного контура. Принцип работы такого детектора изображен на рис. 11.18.

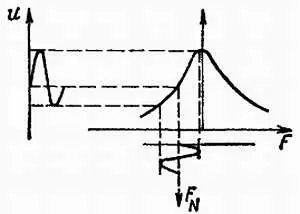
Рис. 11.18. Принцип работы частотного детектора, работающего на скате резонансной кривой

Резонансный контур отстроен от несущей частоты подведенного частотно-модулированного сигнала. Если частота этого сигнала меняется по синусоидальному закону в соответствии с изменением модулирующего сигнала, то ток в контуре также меняется синусоидально, возрастая при приближении частоты сигнала к резонансной частоте контура и убывая при удалении частоты сигнала от значения, соответствующего резонансу. При таком решении выходной сигнал является амплитудно-модулированным. На выходе схемы амплитудного детектирования получаем модулирующий сигнал.

Из-за нелинейности ската амплитудной характеристики резонансного контура и связанных с ней искажений демодулированного сигнала, а также большой чувствительности схемы к амплитуде входного сигнала эта простая схема детектора не используется.

Частотный дискриминатор является одной из наиболее часто используемых схем частотной демодуляции. Схема такого дискриминатора представлена на рис. 11.19.

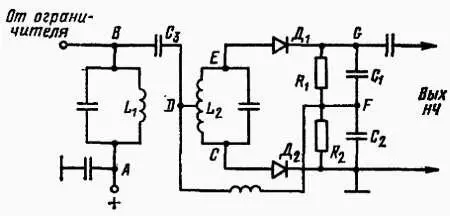
Рис. 11.19. Частотный дискриминатор

Сигнал постоянного уровня подается с ограничителя на связанные резонансные контуры, настроенные на одну и ту же резонансную частоту, равную несущей частоте модулированного колебания. Работа дискриминатора основывается на сдвиге фазы напряжений на первом и втором контурах полосового двузвенного фильтра. Разность фаз этих напряжений составляет 90° на резонансной частоте контуров, а за резонансом изменяется вместе с изменением частоты. Благодаря двойной связи между контурами, индуктивной и непосредственной через конденсатор С 3с большой емкостью, первичное и вторичное напряжения суммируются особым способом и подаются на встречно работающие амплитудные детекторы. Высокочастотный дроссель замыкает цепь для постоянного тока.

Переменное напряжение, подведенное к верхнему диоду Д 1, является векторной суммой первичного напряжения АВ и половины вторичного напряжения DE , изображенной вектором М (рис. 11.20).

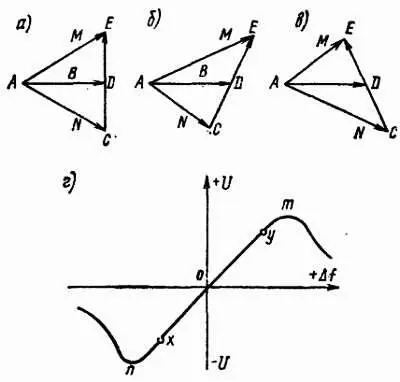
Рис. 11.20. Принцип действия фазового дискриминатора:

а— векторная диаграмма при f = f0; б— векторная диаграмма при f> f0; в— векторная диаграмма при f< f0; г— характеристика дискриминатора