И. Хабловски - Электроника в вопросах и ответах

В двоичной системе счисления любое число удается записать с помощью 1 или 0, например двоичное число 11101011 соответствует десятичному числу 235. Каждая позиция числа, записанного в двоичной системе счисления, представляет одно из двух состояний (1 или 0). В электронике имеются элементы (транзистор, лампа, диод), которые могут работать в двух состояниях: пропускания (включено) и непропускания (выключено). Например, цепь тока — состояние включения и состояние выключения, реле — состояние замыкания и состояние размыкания.

Относительно электрических сигналов двоичная система счисления также соответствует двум состояниям или двум уровням: высокому (более положительному) и низкому (менее положительному, нулевому или даже отрицательному). Если высокое состояние рассматривать как «1», а низкое как «0», то имеем так называемую положительную логику. При таком условии каждое из двух возможных состояний элемента или схемы условно обозначается следующим способом (рис. 12.2): состояние H(от англ. high —высокий) или 1— да — элемент активный; состояние L(от англ. low — низкий) или 0— нет — элемент пассивный. В случае отрицательной логики высоким уровням присваивается 0, а низким 1. В дальнейшем примем только положительную логику.

На практике невозможно осуществить такое условие, при котором все цифровые сигналы точно соответствуют одному из двух принятых уровней, и разрешаются некоторые допуски, так что следовало бы скорее говорить о двух интервалах, в которых находятся сигналы.

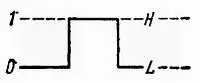
Рис. 12.2. Интерпретация уровней цифрового сигнала в положительной логике

Объяснение двоичной системы проще всего провести сравнением с широко используемой в других областях десятичной системой.

Как известно, в десятичной системе для записи чисел используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиция (положение) каждой цифры в числе, записанном в десятичной системе, определяет ее значение, например цифра 3 в числе 235 определяет три десятка, т. е. 30, а цифра 3 в числе 2350 определяет три сотни, т. е. 300.

Для этих примеров можно записать:

235 = 2·10 2+ 3·10 1+ 5·10 0;

2350 = 2·10 3+ 3·10 2+ 5·10 1+ 0·10 0.

Как легко заметить, в десятичной системе каждое число записывается как последовательность коэффициентов при последовательных степенях основания этой системы.

В двоичной системе основание равно двум и имеются только две цифры 1 и 0. Последовательность цифр в двоичной записи числа представляет собой коэффициенты при соответствующих степенях двойки.

Например, имеем:

0 = 0·2 3+ 0·2 2+ 0·2 1+ 0·2 0, т. е. 0000;

1 = 0·2 3+ 0·2 2+ 0·2 1+ 1·2 0, т. е. 0001;

2 = 0·2 3+ 0·2 2+ 1·2 1+ 0·2 0, т. е. 0010;

3 = 0·2 3+ 0·2 2+ 1·2 1+ 1·2 0, т. е. 0011;

4 = 0·2 3 + 1·2 2+ 0·2 1+ 0·2 0, т. е. 0100;

15 = 1·2 3+ 1·2 2+ 1·2 1+ 1·2 0, т. е. 1111;

235 = 1·2 7+ 1·2 6+ 1·2 5+ 0·2 4+ 1·2 3+ 0·2 2+ 1·2 1+ 1·2 0= (128 + 64 + 32 + 0 + 8 + 0 + 2 + 1), т. е. 11101011.

Как видно из приведенных выше примеров, двоичная запись, образованная из четырех цифр, это четырехбитовая запись. Она позволяет записать лишь числа от 0 до 15 (2 3+ 2 2+ 2 1+ 2 0= 8 + 4 + 2 + 1), и на этом ее емкость исчерпывается. В связи с этим в цифровой технике часто пользуются и другими двоичными системами, представляющими модификацию «чистой» системы, т. е. двоичной системы, обозначаемой обычно как 8421.

Часто применяется двоично-десятичный код. Он основан на том, что каждую цифру числа, записанного в десятичной системе, записывают отдельно с помощью четырех битов. Поясним это на примере числа 235 (табл. 12.1).

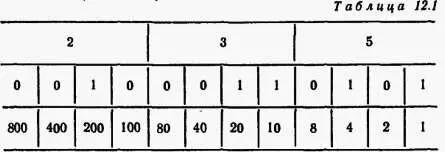
Достоинством двоично-десятичной системы является упрощение замены чисел, записанных в десятичной системе, числами, записанными в двоичной системе, и наоборот.

Очевидно, что действия с двоичными числами отличны от операций, которые выполняют с числами, записанными в десятичной системе. Они очень просты и легки для запоминания.

Сложение чисел, записанных в двоичной системе, выполняется в соответствии со следующим правилом (или иначе алгоритмом):

0 + 0 = 0;

0 + 1 = 1;

1 + 0 = 1;

1 + 1 = 0 с переносом единицы на следующую позицию влево.

Последний алгоритм имеет сходство со сложением в десятичной системе, когда результат сложения больше или равен 10,

Вычитание осуществляется согласно следующему алгоритму:

0 — 0 = 0;

0 — 1 = 1 и затем со следующей позиции (похоже на ситуацию в десятичной системе);

1 — 1 = 1;

1 — 1 = 0.

Умножение чисел в двоичной системе производится очень просто. Вместо большой таблицы умножения в десятичной системе в двоичной имеем маленькую и легкую для запоминания таблицу

0·0 = 0;

1·0 = 0;

0·1 = 0;

1·1 = 1.

Деление двоичных чисел обычно заменяется умножением, и при этом используются приведенные выше алгоритмы.

Логическим элементом, или функтором, называется элемент, принимающий значения 0 и 1. В нем существует определенная логическая связь между входным и выходным сигналами. Связь между сигналами определяется логической функцией. Для математического описания логической функции используется булева алгебра.

Основными логическими операциями этой алгебры являются: отрицание, логическое умножение (конъюнкция), логическое сложение (дизъюнкция). Существуют и другие логические операции.

Обозначим через хнекоторое утверждение или состояние Ипримем, что если хистинно, то можно записать х= 1, а если хложно, то х= 0. Введем еще одно утверждение или состояние у и также примем, что у= 1, если у истинно, и у= 0, если у ложно.

Основой логического умножения

z = х· у,

где z— логическое произведение, причем «·» означает именно логическую операцию, а не арифметическое действие, является анализ утверждения, что хи уистинны.

Рассмотрим четыре возможных случая:

Случай 1. Примем: х= 1; у= 1. Это означает, что хистинно, уистинно. Очевидно, утверждение « хи уистинны» также является истинным, что записываем следующим образом: z= х· у= 1.

Резюмируем, для х = 1 и у= 1 z = х· у= 1.

Случай 2. Примем: х= 1; у= 0. В этом случае сделанное утверждение z = х· уложно, т. е. z = х· у= 0.