И. Хабловски - Электроника в вопросах и ответах
- Название:Электроника в вопросах и ответах
- Автор:
- Жанр:
- Издательство:Радио и связь
- Год:1984
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
И. Хабловски - Электроника в вопросах и ответах краткое содержание
В книге популярно в форме вопросов и ответов объясняются физические основы электроники, электронные компоненты и схемы, особенности их применения. Удачно сочетается широта тематики — от дискретных полупроводниковых приборов до интегральных микросхем с простотой и наглядностью изложения материала.
Для широкого круга читателей.
Электроника в вопросах и ответах - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Резюмируем: для х= 1 и у= 0 z = х· у= 0.
Случай 3. Примем: х= 0; у= 1. В этом случае утверждение z = х· уложно, как в случае 2, и можем записать для х= 0 и у= 0 z = х· у= 0.
Случай 4. Примем: х= 0; у= 0, и тогда z = х· у= 0, Рассмотренные случаи можем cвести в табл. 12.2
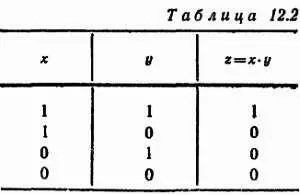
Как легко заметить, приведенная таблица идентична «таблице умножения», обязательной в двоичной системе и приведенной, выше.
Как осуществить функцию логического умножения?
Функция логического умножения, называемая также конъюнкцией, реализуется логическим элементом (функтором) И, элементом типа И и осуществляется в виде схемы, которая дает на выходе единицу тогда и только тогда, когда сигналы на обоих входах логического элемента имеют значение, соответствующее единице. Это совпадает с табл. 12.2. Самым простым способом такую функцию можно реализовать с помощью схемы, состоящей из двух реле, включенных последовательно (рис. 12.3). При этом можно получить четыре случая, описанных правилами логического умножения, причем один из них вызывает появление выходного сигнала.
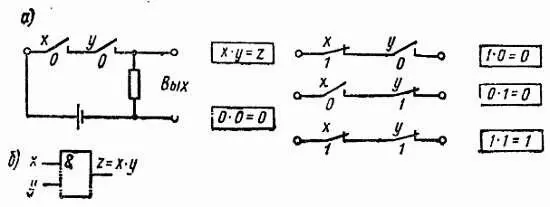
Рис. 12.3. Пример простого осуществления функции И( а) и графическое обозначение элемента И( б)
На рисунке приведено функциональное обозначение элемента типа И, встречающееся в литературе и используемое для обозначений на электрических схемах. Чаще всего применяется функциональное обозначение.
Очевидно, что функцию И можно реализовать и другим способом — чисто электронным путем. Это будет рассмотрено ниже.
Что такое операция логического сложения?
Как в случае логического умножения исходим из некоторого сделанного утверждения. Для операции логического сложения — это утверждение, что хили уистинны» Запишем это следующим способом: z= х+ у, причем знак «+» означает, как и ранее, знак «·», только логическую операцию, а не арифметическое действие. Такое утверждение является действительно истинным тогда, когда по крайней мере только хили только уистинны, а также и в случае, когда хи уодновременно истинны. Возможны четыре случая» сведенные в табл. 12.3:
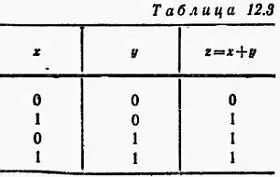
Как осуществить функцию логического сложения?
Функция логического сложения, называемая также дизъюнктцией, реализуется логическим элементом типа ИЛИв виде схемы, которая дает на выходе единицу, если это значение имеет по крайней мере один из входных сигналов. Это соответствует табл. 12.3. Самым простым способом такую функции можно реализовать с помощью схемы, образованной двумя реле, включенными параллельно, как показано на рис. 12.4. На этом же рисунке указано также графическое обозначение элемента типа ИЛИ.
Другие функциональные схемы, реализующие функцию ИЛИ, приводятся ниже.
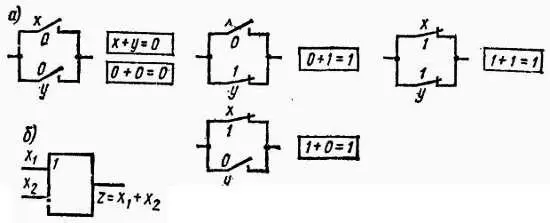
Рис. 12.4. Пример осуществления функции ИЛИ( а) и условное графическое обозначение элемента ИЛИ( б)
Что такое операция отрицания?
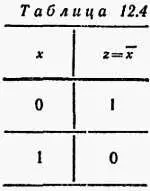
Исходим из утверждения, что хложно, выражаемого также сокращенно «не х» и записываемого следующим образом: z= х¯. Это утверждение правильно только тогда, когда х = 0. Следовательно, имеются два случая (табл. 12.4).
Как реализовать операцию отрицания?
Операция отрицания или инверсии, называемая также функцией НЕили элементом типа НЕ, осуществляется в виде схемы, изменяющей логическое значение входного сигнала на противоположное, например схемы, дающей на выходе сигнал 1, когда на входе 0, и наоборот. Такую функцию можно реализовать, например, с помощью усилителя, инвертирующего фазу сигнала. Графическое изображение элемента типа НЕпредставлено на рис. 12.5.
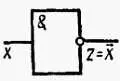
Рис. 12.5. Условное графическое обозначение элемента НЕ
Что такое элемент типа ИЛИ — НЕ?
Это логический элемент [26] Логические элементы, реализующие функции И, ИЛИ, НЕ, И — НЕ, ИЛИ — HЕ, относятся к одноступенчатой логике. — Прим. ред .
, реализующий отрицание логического сложения (функция Пирса ) или, что в конечном результате равнозначно, реализующий произведение отрицаний; запишем это следующим образом:
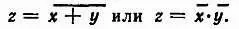
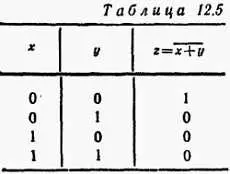
Следовательно, это элемент, представляющий собой соединение двух функций, отсюда название ИЛИ — НЕ. Элемент ИЛИ — НЕ дает на выходе единицу тогда и Только тогда, когда на обоих входах присутствует сигнал 0. Это можно представить в виде табл. 12.5.
Графическое изображение элемента типа ИЛИ — НЕ показано на рис. 12.6. Как следует из записи функции, элемент ИЛИ — НЕ можно реализовать соединением элементов ИЛИ и НЕ либо соединением двух элементов НЕ с элементом И (рис. 12.7). Более того, можно показать, что при использовании элементов ИЛИ — НЕ удается реализовать любую переключающую функцию. Примеры практических решений элементов типа ИЛИ — НЕ приведены на рис. 12.10, в , 12.11.
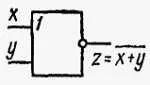
Рис. 12.6. Условное графическое обозначение элемента ИЛИ — НЕ
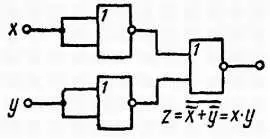
Рис. 12.7. Функция Ипри использовании элементов типа ИЛИ — НЕ
Что такое элемент И — НЕ?
Это элемент, реализующий отрицание логического умножения (функцию Шеффера ) или, что равнозначно в конечном результате, сумме отрицаний. Запишем эту функцию следующим образом:
Читать дальшеИнтервал:
Закладка:










