Пауль Хоровиц - Искусство схемотехники. Том 3 [Изд.4-е]

Микроволновые счетчики. Используя современные цифровые интегральные схемы, можно работать с частотами порядка 3 ГГц. В частности, фирма GigaBit Logic выпускает серию счетчиков с чрезвычайно высоким быстродействием — до 3 ГГц. На более высоких частотах можно использовать гетеродинный метод для смешения микроволнового входного сигнала с частотой счета, или так называемый метод переходного генератора, при котором входной сигнал «захватывается» по фазе n -й гармоникой ГУН, затем частота ГУН измеряется и умножается на n .

Ошибка при счете ±1. Недостаток представленной счетной схемы состоит в том, что на низких частотах нельзя обеспечить высокую точность из-за того, что при счете имеет место ошибка, равная ±1. Например, если частота сигнала равна приблизительно 10 Гц, а время стробирования составляет 1 с, то результат будет правильным только на 10 %, так как вы получите или 9, или 10, или 11. Можно производить измерение на более длинном интервале времени, но вам понадобится целый день, чтобы получить приличную точность (определяемую отношением 1:10 6), а если бы частота сигнала была равна, например, 1 МГц, то для проведения измерений потребовалась бы всего одна секунда. Существует несколько способов решения этой задачи: измерение периода (вместо частоты), использование методов интерполяции, использование ФАПЧ с умножением частоты.

Два первых способа мы рассмотрим в следующих разделах, так как на самом деле их нельзя отнести к непосредственным измерениям частоты.

На рис. 15.26 показано применение схемы ФАПЧ для измерения частоты методом «увеличения разрешающей способности с помощью умножения частоты».

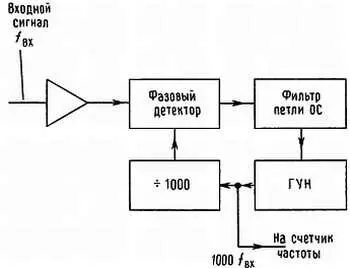
Рис. 15.26. Увеличение разрешающей способности при измерениях низких частот с помощью схемы ФАПЧ.

Стандартная схема ФАПЧ синтезирует частоту, которая превосходит частоту входного сигнала, скажем, точно в 100 раз, затем такой сигнал поступает на счетчик, работу которого мы описали выше. На точность этого метода накладывает ограничение «дребезг фазы» в фазовом детекторе и компенсационные параметры петли. Например, если сигнал, имеющий частоту 100 Гц, умножается на 1000, время счета составляет 1 с, а дребезг в фазовом детекторе оценивается величиной 1 % за цикл (3,6°) иле 100 мкс, то точность измерения будет определяться отношением 1:100000, хотя разрешающая способность оценивается отношением 1:1000000.

А теперь мы скажем несколько слов о двух других способах повышения точности при измерении частоты: речь идет об измерениях периода и о методе интерполяции при измерениях временных интервалов.

Измерение периода («обратный счет»).Один из способов повышения разрешающей способности при измерении низких частот состоит в том, что входной сигнал (или некоторая его часть) используется для стробирования часов. На рис. 15.27 показана стандартная схема такого счетчика периода.

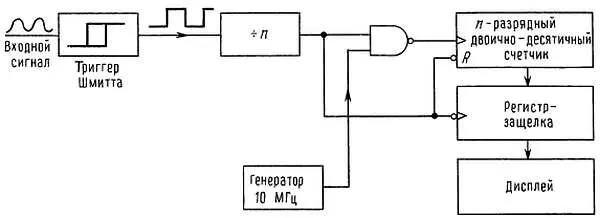
Рис. 15.27. Схема измерения периода.

Число периодов измерения обычно можно задавать с помощью переключателя в виде одной из степеней основания 10 (1, 10, 100 и т. д.). Обычно число периодов выбирают так, чтобы измерения занимали удобный отрезок времени, как правило 1 с, а полученный за это время результат должен содержать около семи значащих цифр. Само собой разумеется, результат будет измеряться в единицах времени, а не частоты, поэтому необходимо выполнить обратный пересчет для получения искомого значения. Для того чтобы выполнить преобразование, не нужно даже уметь делить, так как в современных счетчиках используют микропроцессоры, предназначенные для выполнения преобразования периода в частоту.

Отметим, что точность измерений периода существенно зависит от стабильности срабатывания триггера Шмитта и от отношения сигнал/шум. Сказанное иллюстрирует рис. 15.28.

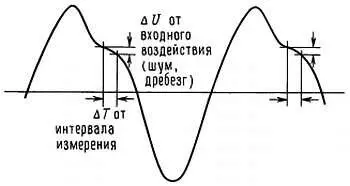
Рис. 15.28.

Основное достоинство метода «обратного счета» состоит в том, что он обеспечивает постоянное разрешение Δf / f для заданной продолжительности измерения независимо от входной частоты. С помощью графика, изображенного на рис. 15.29, можно сравнить разрешающую способность частотного и периодического (обратного счета) методов измерения частоты при продолжительности измерения, равной 1 с, и при использовании таймера с частотой 10 МГц.

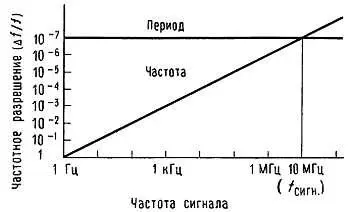
Рис. 15.29. Разрешающая способность для счетчиков частоты и периода.

График, соответствующий методу периода, на самом деле должен представлять собой слегка волнистую линию, так как обычно приходится иметь дело с приближениями к степени числа 10 для осредняемого числа периодов. Но даже этот недостаток отходит в область предания с появлением «умных» счетчиков» на микропроцессорах (например, дешевый счетчик фирмы Hewlett-Packard типа 5315А), которые обеспечивают плавную регулировку времени стробирования; они сами знают, по какому числу периодов производилось осреднение, и самостоятельно выполняют деление результата на нужное число. Кроме того, они сами определяют, когда необходимо перейти от режима измерений периода к режиму прямого измерения частоты. Такое переключение выполняется в том случае, когда входная частота превышает частоту таймера и позволяет получать оптимальное разрешение при любой частоте входных сигналов.

Еще одно достоинство метода измерений частоты по периоду состоит в возможности внешнего управления временем стробирования. Это достоинство проявляется, например, когда возникает необходимость измерить частоту короткого тонового импульса. В этом случае простой счетчик частоты даст неправильный результат, так как его интервал стробирования не совпадает с импульсом. Метод счета периода позволяет стробировать измерения извне и даже за счет высокой разрешающей способности выполнять измерения в различных точках импульса.

Возникает вопрос: можно ли получить более высокую разрешающую способность, чем Δf / f ~= 1/ f таймераT (для периодических измерений) или 1/ f входаT (для частотного счетчика) при относительной ошибке по частоте, равной Δf / f для интервала счета Т ? Оказывается, можно. На практике применяют несколько хитроумных схем. Некоторые из них мы рассмотрим в следующем подразделе (посвященном измерению временных интервалов), а сейчас, просто для того чтобы показать, как можно этого добиться, мы приводим рис. 15.30, который иллюстрирует метод измерения частоты 1 МГц — генератора с разрешающей способностью 1:10 12при продолжительности измерений, равной 1 с.