Пауль Хоровиц - Искусство схемотехники. Том 3 [Изд.4-е]

Модуль комплексного числа равен

| N| = | а + bi | = [( а + bi )( a — bi )] 1/2= ( а 2+ Ь 2) 1/2, т. е. | N| = ( NN*) 1/2.

Для того чтобы определить модуль комплексного числа, нужно умножить это число на сопряженное и взять квадратный корень от произведения. Модуль произведения (или частного) двух комплексных чисел представляет собой просто произведение (или частное) их модулей.

Для действительной и мнимой частей комплексного числа иногда используется следующая запись:

действительная часть N= Re( N),

мнимая часть N= Im( N).

Для того чтобы получить действительную или мнимую часть, нужно записать число в виде а + bi и взять а или b . При этом может потребоваться выполнить умножение или деление, так как комплексное число может быть весьма запутанным.

Для представления комплексных чисел иногда используют комплексную плоскость. Она представляет собой такую же плоскость, как и плоскость с координатами х, у . При изображении комплексного числа действительная часть берется как координата х , а мнимая — как у , т. е. на этой плоскости используются оси ДЕЙСТВИТЕЛЬНАЯ ( х ) и МНИМАЯ ( у ), как показано на рис. Б.1.

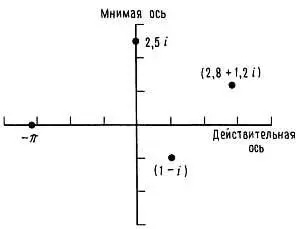
Рис. Б.1.

Используя эту аналогию, иногда комплексные числа записывают с помощью координат х, у :

а + bi <-> ( a, b ).

Как и обычные точки с координатами х, у , комплексные числа можно представлять в полярных координатах; это представление называют тригонометрическим. Например, число а + bi можно записать и так (рис. Б.2):

a + bi = ( R, θ ),

где R = (а 2+ b 2) 1/2и = arctg( b / a ).

Если учесть, что

e ix = cos x + i sin x

(это выражение, известное под названием формулы Эйлера, нетрудно получить, если представить экспоненциальную функцию в виде ряда Тейлора), то получим показательную форму записи:

N= a + bi = Re iθ ,

R = | N| = ( NN*) 1/2= ( а 2+ b 2) 1/2,

θ = arctg( b / a ),

т. е. модуль комплексного числа R и угол θ — это просто полярные координаты точки, представляющей число на комплексной плоскости. Показательная (или полярная) форма представления удобна для выполнения операций умножения (или деления) комплексных чисел - модули чисел перемножаются (делятся), а углы — аргументы складываются (вычитаются):

( ae ib )( ce id ) = ace i(b+d) .

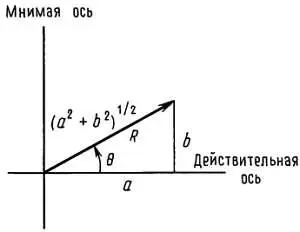
Рис. Б.2.

И наконец, для того чтобы перейти от представления в полярных координатах к представлению в прямоугольных координатах, следует просто воспользоваться формулой Эйлера:

ae ib = a cos b + ia sin b ,

т. е. Re(ae ib) = a cos b , Im( ae ib ) = a sin b .

Для того чтобы умножить комплексное число на экспоненциальную функцию, необходимо просто выполнить соответствующие операции умножения:

N= a + bi ,

N ix = ( а + bi ) (cos х + i sin х ) = ( a cos x — b sin x ) + i ( b cos x + a sin x ).

Дифференциальное исчисление

Начнем с понятия функции f( x ), т. е. формулы, которая для каждого значения х позволяет найти значение у= f( x ). Функция f( х ) является однозначной, если каждому значению х она ставит в соответствие единственное значение у . Понятие функции у= f( x ) иллюстрирует график, представленный на рис. Б.З.

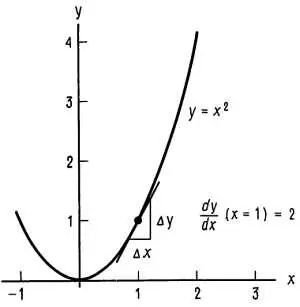
Рис. Б.3.

Производная у по х определяется углом наклона графика у к оси х . Если вы проведете касательную к графику функции в некоторой точке, то наклон касательной в этой точке и есть dy / dx , т. е. производная сама по себе представляет функцию, так как ее значение определено в каждой точке. На рис. Б.З наклон в точке (1,1) определяется значением 2, а в точке начала координат он нулевой (немного ниже сказано, как вычисляется производная).

Пользуясь математическими терминами, можно сказать, что производная - это предел, к которому стремится отношение приращения у( Δу ) к приращению х( Δ х), когда Δ х стремится к нулю.

Процитируем песенку, которую когда-то сочинили по этому поводу в Гарвардском университете (авторы Том Лехрер и Льюис Бранском):

(На мелодию «Что-то должно измениться». W. Benton Overstreet.)

Дифференцирование - это прямая операция, и для основных функций составлены стандартные таблицы производных. Ниже приводятся основные правила нахождения производных ( u и v — это функции х ):

Некоторые производные

Последнее правило представляет собой правило дифференцирования сложной функции, оно распространяется на цепочку из любого числа функций и очень полезно для вычисления производных. Иногда функцию дифференцируют, чтобы определить значение производной в некоторой точке. В других случаях требуется найти минимум или максимум функции. Так как в точке экстремума производная равна нулю, то найденную производную приравнивают к нулю и разрешают полученное уравнение относительно х .

Рассмотрите следующие примеры:

Маломощные проволочные и пленочные резисторы с допуском от 2 до 20 % имеют стандартные значения сопротивлений и стандартную схему цветной маркировки. У начинающего это может вызвать подозрения, но на самом деле такая маркировка позволяет легко определить сопротивление стоящего в схеме резистора по его цвету, а не по цифровой маркировке, которую не сразу разглядишь. Стандартные значения сопротивлений резисторов выбраны так, что смежные значения отличаются на 10 % для резисторов с допуском 2 и 5 % и на 20 % для допусков 10 и 20 %. С помощью цветной маркировки можно задать многие значения сопротивлений, но не все они существуют на практике.