Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

С целью конкретизации этих идей, давайте рассмотрим оба примера проектирования как последовательностных, так и комбинационных схем, используя язык CUPL.

Пример использования языка CUPL для проектирования преобразователя из 7-сегментного кода в шестнадцатеричный (комбинационная логика). Наступает время, когда вы захотите использовать желаемый БИС-кристалл, который выполняет определенную функцию (например, калькулятор или хронометр), как часть создаваемого вами устройства. Беда в том, что эти БИС-кристаллы обычно имеют выходы для прямого управления 7-сегментным индикатором, который предпочтительней, чем шестнадцатеричные (или двоичные) выходы, которые вы хотите получить. Давайте спроектируем кристалл-шифратор, который преобразует 7-сегментный код обратно в 4-битовый двоичный, такая функция не реализуется как стандартная микросхема (хотя существует дешифратор из семисегментного кода в двоично-десятичный, 74С915).

Входы представляют отдельные сегментные сигналы, которые всегда помечаются символами a — f (рис. 8.76).

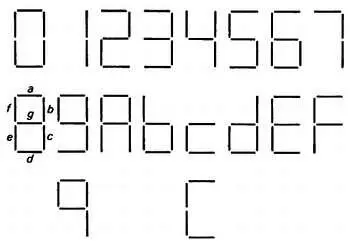
Рис. 8.76. Коды 7-сегментного индикатора.

На рис. 8.76 показано, как цифры представляются на 7-сегментном индикаторе. Заметьте, что возможно двоякое представление «9» и «С», оба из которых должны корректно восприниматься вашей логикой. Для ПМЛ мы выбираем X6L8, 20-контактная комбинационная часть которой логически была показана на рис. 8.45.

Рис. 8.77 представляет входное описание на языке CUPL. Здесь сигналы запуска сегментов а — g обозначают входы (положительная логика), а шестнадцатеричные разряды D0-D3 выходы (отрицательная логика). Язык CUPL позволяет определить промежуточные переменные, которые могут быть использованы в выражениях позднее. В этом случае удобно определить очевидные переменные от zero до next через возможные отображения цифры в терминах сегментных входов. Это просто большие термы произведений (И) от входных сегментных переменных, которые вы можете прочесть из изображений цифр на рис. 8.76.

/** Inputs **/

PIN 1 = a; /* segment a */

PIN 2 = b; /* segment b */

PIN 3 = c; /* segment c */

PIN 4 = d; /* segment d */

PIN 5 = e; /* segment e */

PIN 6 = f; /* segment f */

PIN 7 = g; /* segment g */

/** Outputs **/

PIN 19 = !D3; /* msb of hex encode */

PIN 18 = !D2; /* */

PIN 17 = !D1; /* */

PIN 16 = !D0; /* 1sb */

/** Declarations and Intermediate Variable Definitions **/

zero = a & b & c & d & e & f & !g;

one = !a & b & с & !d & !e & !f & !g

two = a & b & !с & d & e & !f & g;

three = a & b & c & d & !e & !f & g;

four = !a & b & с & !d & !e & f & g;

five = a & !b & с & d & !e & f & g;

six = a & !b & c & d & e & f & g;

seven = a & b & с & !d & !e & !f & !g;

eight = a & b & c & d & e & f & g;

nine = a & b & с & !d & !e & f & g

# a & b & c & d & !e & f & g; /* two ways */

hexa = a & b & с & !d & e & f & g;

hexb = !a & !b & c & d & e & f & g;

hexc = !a & !b & !c & d & e & !f & g

# a & !b & !c & d & !e & f & !g; /* two ways */

hexd = !a & b & c & d & e & !f & g;

hexe = a & !b & !c & d & e & f & g;

hexf = a & !b & !c & !d & e & f & g;

/** Logic Equations **/

D3 = eight # nine # hexa # hexb # hexc # hexd # hexe # hexf;

D2 = four # five # six # seven # hexc # hexd # hexe # hexf;

D1 = two # three # six # seven # hexa # hexb # hexe # hexf;

D0 = one # three # five # seven # nine # hexb # hexd # hexf

Рис. 8.77. Спецификация преобразователя 7-сегментного представления в 16-ричное на языке CUPL.

Окончательно каждый двоичный выходной бит записывается как сумма (ИЛИ) цифровых переменных, при которых этот бит устанавливается. Мы используем уровни отрицательной логики, потому что 16L8 представляет матрицу И-ИЛИ-НЕ. Этим заканчивается логическая спецификация для языка.

Упражнение 8.29.Проверьте для себя правильность нашей работы, записав некоторые из отображаемых символов, через заданные нами промежуточные переменные zero-next .

Язык CUPL сначала использует определение промежуточных переменных для записи выражений D0-D3 прямо в термах входных переменных a — f , работа, которая подобно ассемблеру PALASM должна исполняться нами изначально. В этом случае логические уравнения представлены в желательной И-ИЛИ-НЕ форме. Однако мы не закончили на этом, так как 16L8 (и все другие комбинационные ПМЛ) допускают не более 7 термов произведений для каждой суммы, тогда как мы имеем 9, 8, 9 и 10 соответственно для выходов D0-D3. Одним решением может быть связывание выхода через вторичный вентиль ИЛИ, для того чтобы получить желательное число термов произведений в сумме.

Эта обычно рассматриваемая форма плоха, так как она удваивает задержки распространения, хотя это не так важно в медленных устройствах, подобных этому. Лучшее решение — произвести логическую минимизацию, используя логическую эквивалентность по формуле Моргана, например.

Мы запускаем минимизатор CUPL, который выдает термы произведений (рис. 8.78).

** Expanded Product Terms **

D0 =>

a & b & c & d & !e & g

# a & b & с & !e & f & g

# a & с & d & !e & f & g

# b & с & !d & !e & !f & !g

# !a & !b & c & d & e & f & g

# a & !b & !c & !d & e & f & g

# !a & b & c & d & e & !f & g

D1 =>

a& !b & !c & e & f & g

# !b & c & d & e & f &g

# a & b & с & !d & e & f & g

# a & b & !c & d & e & !f & g

# a & b & c & d & !e & !f & g

# a & b & с & !d & !e & !f & !g

D2 =>

а & !b & !с & d & е & f

# а & !b & c & d & f & g

# а & !b & !с & е & f & g

# !а & b & с & !d & !е & f & g

# !a & b & c & d & e & !f & g

# !a & !b & !c & d & e & !f & g

# a & b & с & !d & !e & !f & !g

D3 =>

a & b & c & f & g

# a & !b & !c & d & e & f

# a & !b & !c & e & f & g

# !a & !b & c & d & e & f & g

# !a & b & c & d & e & !f & g

# !a & !b & !c & d & e & !f & g

D0.oe => 1

D1.oe => 1

D2.oe => 1

D3.oe => 1

Рис. 8.78. Преобразователь 7-сегментного представления в 16-ричное с минимизированными термами произведения.

Взгляните, все удовлетворяет ограничению «7 произведений». CUPL также рисует для вас карту перемычек (рис. 8.79).

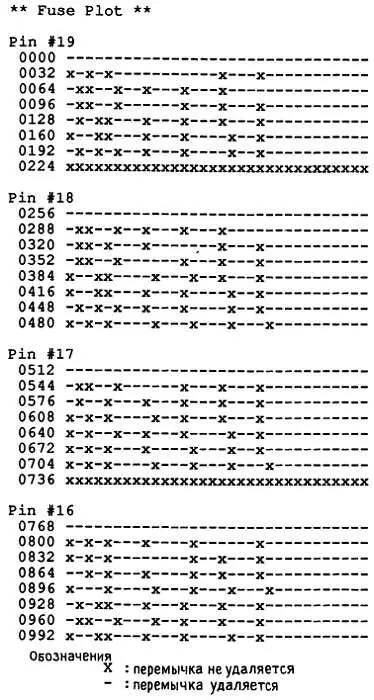
Рис. 8.79.Карта перемычек преобразователя 7-сегментного представления в 16-ричное.

Конечно, вы не программируете ПМЛ так, а используете вместо этого прямую загрузку универсального JEDEC программирующего формата. В этом примере язык CUPL, очевидно, делает трудную задачу простой.

Пример использования языка CUPL для программирования автомата-продавца (последовательная схема). Произвольная машина состояний ( разд. 8.18 ) имеет набор состояний и правил перехода для движения между этими состояниями по каждому фронту синхроимпульса. Правила перехода зависят от текущего состояния и от частной комбинации входных уровней, существующих на следующем фронте. Вы можете соорудить машину состояний на программируемой логике, содержащей регистры, если а) существует достаточное число битов в регистре для представления всех возможных состояний (например, с 4-разрядным регистром вы можете иметь до 16 состояний), и б) существует достаточное число входов и логических вентилей для реализации правил перехода.

Как пример, давайте спроектируем регистровую ПМЛ для диаграммы состояний на рис. 8.80.

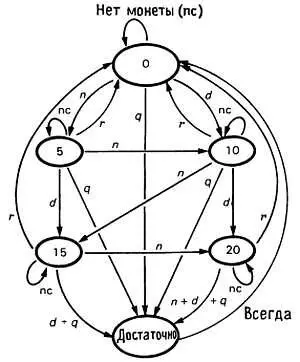
Рис. 8.80. Диаграмма состояний торгового автомата.