Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Упражнение 1.20. Покажите, что последовательное подключение конденсатора емкостью С= 1/ ω 2 Lк последовательной RL-цепи делает коэффициент мощности этой цепи равным единице. Затем рассмотрите параллельную цепь и параллельно подключенный конденсатор.

Делители напряжения: обобщение.Простейший делитель напряжения (рис. 1.5) состоит из пары последовательно соединенных резисторов. Входное напряжение измеряется в верхней точке относительно земли, а выходное-в точке соединения резисторов относительно земли. От простейшего резистивного делителя перейдем к более общей схеме делителя, если один или оба резистора заменим на конденсатор или индуктивность, как, на рис. 1.51 (в более сложной схеме присутствуют и R , и L , и С ).

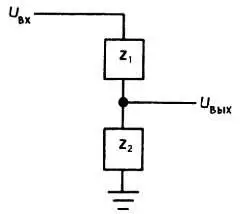
Рис. 1.51. Обобщенная схема делителя напряжения: пара электрических цепей с произвольным импедансом.

Вообще говоря, в таком делителе отношение U вых / U вх не является постоянной величиной, а зависит от частоты. Анализ схемы выполняется без всяких хитроумных приемов:

I= U вх/ Z полн,

Z полн = Z 1+ Z 2,

U вых= Z 2= U вх[ Z 2/( Z 1+ Z 2)].

Не будем сосредоточивать внимание на полученном результате, рассмотрим лучше некоторые простые, но очень важные примеры.

Благодаря тому что импеданс конденсатора, равный Z С= —j/ ωС, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять. В этом разделе вы познакомитесь с примерами простейших RС-фильтров, к которым мы будем неоднократно обращаться в дальнейшем. В гл. 5 и приложении 3 описаны более сложные фильтры.

Фильтры высоких частот.На рис. 1.52 показан делитель напряжения, состоящий из конденсатора и резистора.

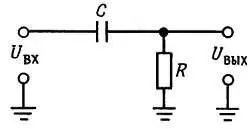
Рис. 1.52. Фильтр высоких частот.

Согласно закону Ома для комплексных величин,

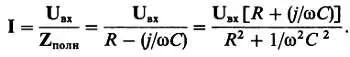
(Окончательный результат получен после умножения числителя и знаменателя на комплексное число, сопряженное знаменателю.) Итак, напряжение на резисторе R равно

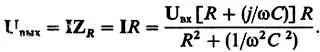
Чаще всего нас интересует не фаза, а амплитуда U вых :

U вых= ( U выхU * вых) 1/2= U вхR/[ R 2+ (1/ ω 2 С 2)] 1/2

U вых= U вхR 1/( R 1+ R 2).

Векторное представление импеданса RС-цепи (рис. 1.53) показано на рис. 1.54.

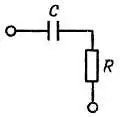
Рис. 1.53.

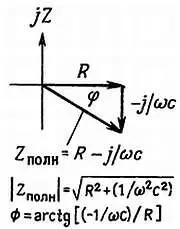
Рис. 1.54.

Итак, если не принимать во внимание сдвиг фаз, а рассматривать только модули комплексных амплитуд, то «отклик» схемы будет определяться следующим образом:

U вых= U вхR[ R 2+ (1/ ω 2 С 2)] 1/2=

= U вх2π f· RC/[1+(2π f· RC) 2] 1/2.

График этой зависимости представлен на рис. 1.55.

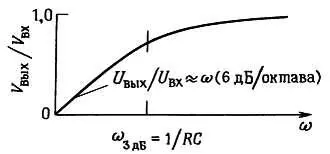
Рис. 1.55. Частотная характеристика фильтра высоких частот.

Такой же результат мы бы получили, если бы определили отношение модулей импедансов как в упражнении 1.17 и в примере перед этим упражнением; числитель представляет собой модуль импеданса нижнего плеча делителя R , а знаменатель-модуль импеданса последовательного соединения R и С .

Как вы видите, на высоких частотах выходное напряжение приблизительно равно входному ( ω >= 1/ RC), а на низких частотах выходное напряжение уменьшается до нуля. Мы пришли к важному результату, запомните его. Подобная схема, по понятным причинам, называется фильтром высоких частот. На практике ее используют очень широко.

Например, в осциллографе предусмотрена возможность связи по переменному току между исследуемой схемой и входом осциллографа. Эта связь обеспечивается с помощью фильтра высоких частот, имеющего перегиб характеристики в области 10 Гц (связь по переменному току используют для того, чтобы рассмотреть небольшой сигнал на фоне большого напряжения постоянного тока).

Инженеры часто пользуются понятием «точки излома» —3 дБ для фильтра (или любой другой схемы, которая ведет себя как фильтр)! В случае простого RС-фильтра высоких частот точка излома —3 дБ определяется выражением:

f 3дБ = 1/2π RC.

Обратите внимание, что конденсатор не пропускает ток ( f = 0). Самый распространенный пример использования конденсатора — это использование его в качестве блокирующего конденсатора постоянного тока. Если возникает необходимость обеспечить связь между усилителями, то почти всегда прибегают к помощи конденсатора. Например, у любого усилителя звуковой частоты высокого класса все входы имеют емкостную связь, так как заранее не известно, какой уровень постоянного тока будут иметь входные сигналы. Для обеспечения связи необходимо подобрать R и С таким образом, чтобы все нужные частоты (в данном случае 20 Гц-20 кГц) поступали на вход без потерь (без деления на входе).

Часто, например при конструировании фильтров, возникает необходимость определить импеданс конденсатора на некоторой частоте. На рис. 1.56 представлен очень полезный график, охватывающий большой диапазон емкостей и частот для зависимости | Z| = 1/2π fC.

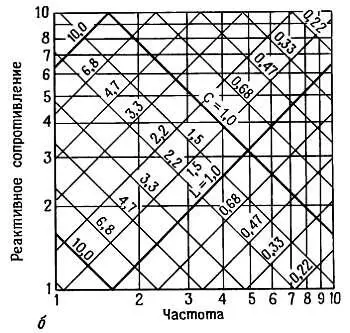
Рис. 1.56. а — Изменение реактивного сопротивления индуктивностей и конденсаторов в зависимости от частоты. Все декады одинаковы и отличаются лишь масштабом, б— Увеличенное изображение одной декады из графика А, график построен для стандартных компонентов, имеющих точность 20 %.

В качестве примера рассмотрим фильтр, показанный на рис. 1.57.

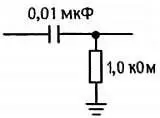
Рис. 1.57.