Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Определение напряжения и тока с помощью комплексных чисел.Только что вы убедились в том, что в цепи переменного тока, работающей с синусоидальным сигналом некоторой частоты, возможен сдвиг по фазе между напряжением и током. Тем не менее если схема содержит только линейные элементы (резисторы, конденсаторы, индуктивности), то амплитуда токов на всех участках схемы пропорциональна амплитуде питающего напряжения. В связи с этим можно попытаться найти некоторые общие выражения тока, напряжения и сопротивления и обобщить тем самым закон Ома.

Очевидно, что для того, чтобы определить ток в какой-либо точке схемы, недостаточно задать одно значение-дело в том, что ток характеризуется как амплитудой, так и сдвигом фазы.

Конечно, можно определять амплитуды и фазовые сдвиги напряжений и токов явно, например U(t)= 23,7·sin(377· t+ 0,38), но оказывается, что проще это делать с помощью комплексных чисел. Вместо того чтобы тратить время и силы на сложение и вычитание синусоидальных функций, можно легко и просто складывать и вычитать комплексные числа. Так как действующие значения напряжения и тока представляют собой реальные количественные величины, изменяющиеся во времени, следует вывести правило для перевода реальных количественных величин в комплексное представление и наоборот. Напомним еще раз, что мы имеем дело с частотой синусоидального колебания ω, и сформулируем следующие правила:

1. Напряжение и ток представляются комплексными величинами U и I .

Напряжение U 0cos(ωt + φ) представляется комплексным числом U 0e jφ . Напомним, что e jθ= cos θ+ jsin θ, где j = √—1.

2. Для того чтобы получить выражение для действующего напряжения и тока, нужно умножить соответствующие комплексные представления на e jωt и выделить действительную часть. Это записывается следующим образом: U( t) = Re( U· e j ωt), Ι( t) = Re( I· e j ωt). Иначе говоря,

(В электронике символ j используется вместо принятого в алгебре для комплексной переменной символа i , с тем чтобы избежать путаницы с током, который также обозначают символом i ). Итак, в общем случае действующие напряжения и токи определяются следующим образом:

U( t) = Re( U· e j ωt) = Re( U)·cos ωt— Im( U)·sin ωt,

Ι( t) = Re( I· e j ωt) = Re( I)·cos ωt— Im( I)·sin ωt,

Например, комплексному напряжению U= 5 jсоответствует реальное напряжение

U( t) = Re[5j·cos ωt+ 5j(j)·sin ωt] = 5sin ωtB

Реактивное сопротивление конденсаторов и индуктивностей.Принятое соглашение позволяет применять закон Ома для схем, содержащих как резисторы, так и конденсаторы, и индуктивности.

Определим реактивное сопротивление конденсатора и индуктивности. Нам известно, U( t) = Re( U 0· e j ωt). Так как в случае конденсатора справедливо выражение I= C( dU/ dt), получим

Ι( t) = — U 0Cω·sin ωt= Re[ U 0· e j ωt/(-j/ ωC)] = Re( U 0· e j ωt/ X C),

т. е. для конденсатора

X C= — j/ ωC,

Х C — это реактивное сопротивление конденсатора на частоте ω . Конденсатор емкостью 1 мкФ, например, имеет реактивное сопротивление —2653 j Ом на частоте 60 Гц и —0,16 j Ом на частоте 1 МГц. Для постоянного тока реактивное сопротивление равно бесконечности. Аналогичные рассуждения для индуктивности дают следующий результат:

X L= j ωL.

Схема, содержащая только конденсаторы и индуктивности, всегда обладает мнимым импедансом; это значит, что напряжение и ток всегда сдвинуты по фазе друг относительно друга на 90°- схема абсолютно реактивна. Если в схеме присутствуют резисторы, то импеданс имеет и действительную часть. Под реактивным сопротивлением подразумевается при этом только мнимая часть импеданса.

Обобщенный закон Ома.Соглашения, принятые для представления напряжений и токов, позволяют записать закон Ома в следующей простой форме:

I= U/ Z, U= I· Z, означающей, что напряжение U , приложенное к схеме с импедансом Z , порождает ток I . Импеданс последовательно и параллельно соединенных элементов определяется по тем же правилам, что и сопротивление последовательно и параллельно соединенных резисторов:

Z = Z 1+ Z 2+ Z 3+…

(для последовательного соединения),

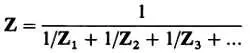
И в заключение приведем формулы для определения импеданса резисторов, конденсаторов и индуктивностей:

Z R= R(резистор),

Z C= —j/ ωC(конденсатор),

Z L = j ωL(индуктивность).

Полученные зависимости позволяют анализировать любые схемы переменного тока с помощью методов, принятых для схем постоянного тока, а именно с помощью закона Ома и формул для последовательного и параллельного соединения элементов. Результаты, которые мы получили при анализе таких схем, как, например, делитель напряжения, сохраняют почти такой же вид. Так же как и для схем постоянного тока, для сложных разветвленных схем переменного тока справедливы законы Кирхгофа; отличие состоит в том, что вместо токов I и напряжений U здесь следует использовать их комплексные представления: сумма падений напряжения (комплексного) в замкнутом контуре равна нулю; сумма токов (комплексных), втекающих в узел, равна сумме токов (комплексных), вытекающих из него. Из последнего правила, как и в случае с цепями постоянного тока, вытекает, что ток (комплексный) в последовательной цепи всюду одинаков.

Упражнение 1.16.Используя формулы для импеданса параллельного и последовательного соединения элементов, выведите формулы ( разд. 1.12 ) для емкости двух конденсаторов, соединенных (а) параллельно, (б) последовательно. Подсказка: допустим, что в каждом случае конденсаторы имеют емкость С1 и С2 . Запишите выражение для импеданса параллельно и последовательно соединенных элементов и приравняйте его импедансу конденсатора с емкостью С . Найдите С .