Иван Шунейко - Пилотируемые полеты на Луну

Вектор цели для компланарной траектории расположен в плоскости второго активного участка (т. е. ?=0), и в процессе выведения к Луне никакого изменения плоскости движения не совершается. Это справедливо для обеих возможностей запуска при компланарных траекториях перелета. Однако, пока ракета-носитель и космический корабль находятся на промежуточной орбите в ожидании второй возможности старта, Луна продолжает двигаться по орбите вокруг Земли в течение дополнительных 90 мин, что приводит к изменению вектора цели. На рис. 31.4 показано перемещение вектора цели,

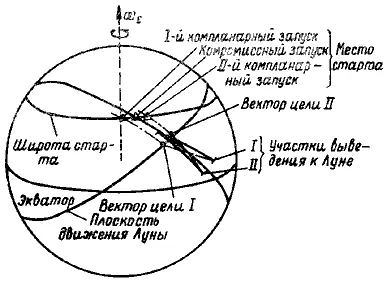
Рис. 31.4. Компромиссная траектория выведения

обусловленное движением Луны, от первой до второй возможности запуска, а также соответствующие моменты старта. Если рассматриваются 2 возможности выведения к Луне, то следует определить общее компромиссное время запуска. По крайней мере для одной из возможностей потребуется выполнить маневр по изменению плоскости движения, так как общее время запуска может удовлетворять условию ?=0 только для одной возможности. На рис. 31.3 показано изменение веса на траектории к Луне и времени запуска для обеих возможностей выведения. Максимальный вес обеспечивается, когда время запуска соответствует компланарному перелету, однако при второй возможности перелета вес оказывается меньше, чем при первой вследствие дренажа газообразного водорода из бака в течение дополнительного оборота на промежуточной орбите. Как видно из графиков, представленных на рис. 31.3, существует только одно время запуска, которое позволяет получить одинаковый вес на траектории к Луне для обеих возможностей. В случае а точка одинакового веса (точка пересечения кривых) расположена между временами двух компланарных запусков. Время запуска, позволяющее получить одинаковую полезную нагрузку, является общим для обеих возможностей и называется здесь компромиссным временем. В случае б точка пересечения двух кривых расположена правее времени компланарного запуска для второй возможности. Это имеет место, когда время между первой и второй возможностями оптимального запуска (?TL) мало. В случае б оптимальным решением для обеих возможностей запуска является время, соответствующее второму компланарному запуску. Процедура выбора компромиссного времени запуска состоит в следующем:

1) рассчитывается траектория для второй возможности компланарного запуска; 2) вычисляется вектор цели для первой возможности компланарного запуска; 3) определяется ?TL; 4) находится компромиссное время запуска, основанное на векторах цели для первой и второй возможностей компланарного запуска.

Отвечающее требованиям прицеливания приближенное значение вектора цели для первой возможности запуска (шаг 2 процедуры) можно вычислить без интегрирования траектории.

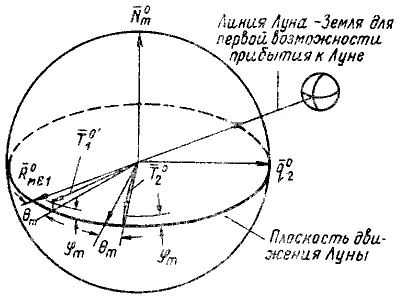
Рис. 31.5. К расчету времени старта для первой возможности.

При этом с помощью системы координат, связанной с плоскостью движения Луны (рис. 31.5), предварительно устанавливается соотношение между вектором цели для второй возможности запуска Т02 и положением линии Луна-Земля в момент, соответствующий прибытию в периселений. Методика вычислений состоит в следующем. Даны величины: R0ME2 – единичный вектор, направленный по линии Луна-Землд в момент прибытия в периселений по компланарной траектории, соответствующей второй возможности запуска и использованию времени для второй компланарной траектории; Т02 – вектор цели для второй возможности компланарного запуска; N0m – единичный вектор, перпендикулярный плоскости движения Луны. Рассмотрим следующие уравнения:

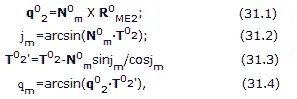
где ?m – единичный вектор, дополняющий N0m и R0ME2 до правой ортогональной системы координат,: ??m – склонение вектора цели Т02 относительно плоскости движения; Т02 – проекция вектора цели на плоскость движения Луны; ?m – прямое восхождение вектора Т02, измеряемое в плоскости движения Луны от линии Луна-Земля, соответствующей моменту прибытия в периселений по второй возможной компланарной траектории.

Предполагается, что вектор цели остается на постоянных угловых расстояниях ?m и ?m от линии Луна-Земля. Если выведение к Луне происходит при первой возможности, а запуск имеет место во время, соответствующее второй возможной компланарной траектории, то положение линии Луна-Земля в момент прибытия в периселений определяется посредством выбора эфемериды, которая сдвинута назад относительно момента прибытия на один период обращения по промежуточной орбите. Вектор цели вычисляется на угловых расстояниях ?m и ?m от результирующего положения линии Луна-Земля, как показано на рис. 31.5. Кроме того отыскивается вектор цели, соответствующий времени первого возможного компланарного запуска, причем должно учитываться дополнительное влияние ?TL. В первом приближении вектор цели Т02' вычисляется без учета влияния ?TL:

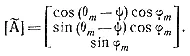
Склонение и прямое восхождение Т01 определяется как

При вычислении вектора цели Т01 будем рассматривать его в качестве функции от ?TL с тем, чтобы можно было применить итерационную процедуру для обеспечения перпендикулярности вектора цели Т01 и нормали к плоскости промежуточной орбиты в случае первой возможности запуска N01 , т. е. совпадения плоскости перелета и промежуточной орбиты. Из уравнения (31.6) при ?TL=0 в первом приближении определяется вектор цели для первой возможности компланарного запуска. Принимая линейную зависимость прямого восхождения и склонения от ?TL, можно получить уравнения для вычисления этих углов по следующим формулам:

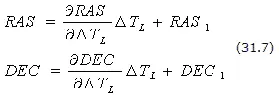
Остальные уравнения, используемые в итерационной процедуре, представлены ниже

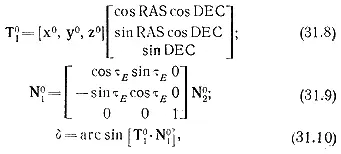
где х 0, у 0, z 0 – единичные векторы системы координат, соответствующей началу ближайшего бесселева года;