Сергей Гаврилов - Расчеты в Excel

Расчеты: Здесь много расчетов связанных с углами. Компьютер угловые функции ведет в радианах.

@010. Угол 180 градусов равен числу Pii = 3,1415926 радиан..

Перевод из градусов в радианы: Радианы = Градусы*Pii/180…

Перевод из радиан в градусы: Градус = Радиан*180/Pii…

Любая тригонометрическая функция требует ввода аргумента в радианах.

Аргумент следует предварительно рассчитать и в функцию вставить адрес ячейки с аргументом.

Формулы приведены выше и в Excel. Можно посмотреть в открытом листе Е14.

Все расчеты проведены в столбике «F»так как много промежеточных расчетов.

Итоговые результаты выведены в столбик результатов «D».

Рисунок вставляем в лист, как описано в @013.

Выполняем защиту столбиков и сохраняем лист как Е 14. Затем сохраняем как Е 14_Z.

Проверим форматирование столбиков и защитим лист @007.

Геометрия радиусной кривой

Все расчеты по разным вариантам исходных данных:

Хорда L; Прогиб Н; Радиус R; Угол G.

Эти расчеты часто требуются для нахождения элементов детали имеющих форму сегмента окружности.

Рис. Геометрия радиусной кривой.

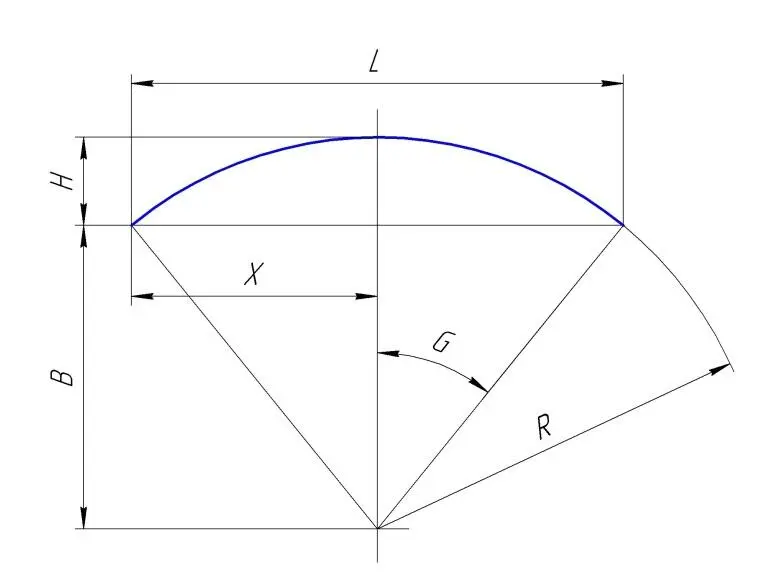
Расчет производим из следующих соотношений:

В = sqrt( R*R – X*X); L = X + X; H = R – B; G = аrcsin ( X / R );

Длина дуги = Pii * R * G / 90;

Площадь сектора Ss = Pii * R * R * G / 180;

Площадь треугольника под хордой St = L * B /2;

Площадь сегмента ( горбушки ) Sg = Ss – St;

Некоторые комбинации данных не позволяют прямого расчета,

тогда применяем метод компьютерного подбора.

Контрольный расчет:

Радиус R = 1000;

Диаметр D = R+R; D = 2000; Хорда L = 765,3668647;

Стрела прогиба максимальная H = 76,12046749;

Угол: Центр – Хорда: 2 * G = Au = 45 градусов..

Площадь сектора круга с углом = Au:

Sk=Pii*D*D* Au /(4*360); Sk = 392699,0816987241;

Площадь треугольника в секторе:

St=(L/2)* B; St = 353553,3905932738;

Площадь горбушки отсеченной хордой:

S = Sk-St; S = 39145,69110545033;

Длина дуги над хордой:

L=Pii*D*Au /360; L = 785,3981634;

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 15. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия радиусной кривой.». Далее форматируем столбики как описано @002. @003. @004. @004А.

Далее как в предыдущем.

Примечание: При исходных данных «Хорда – Прогиб» прямым расчетом не решается – применяем метод подбора с шаговым уточнением. В Excel програмные циклы запрещены – поэтому автоматический подбор запрограммировать не получится. Такие программы делаем в Python..

Координаты радиусной кривой

Построение части окружности методом подъема применяется тогда, когда радиус слишком велик

для традиционного построения, либо когда точка центра радиуса недоступна.

Если внутри контура кривой расположены объекты мешающие построению хорды, тогда строят линию, паралленьную хорде, с точкой касания в вершине кривой и от этой линии откладывают величины «Н2».

Рис. Координаты радиусной кривой.

,,,,

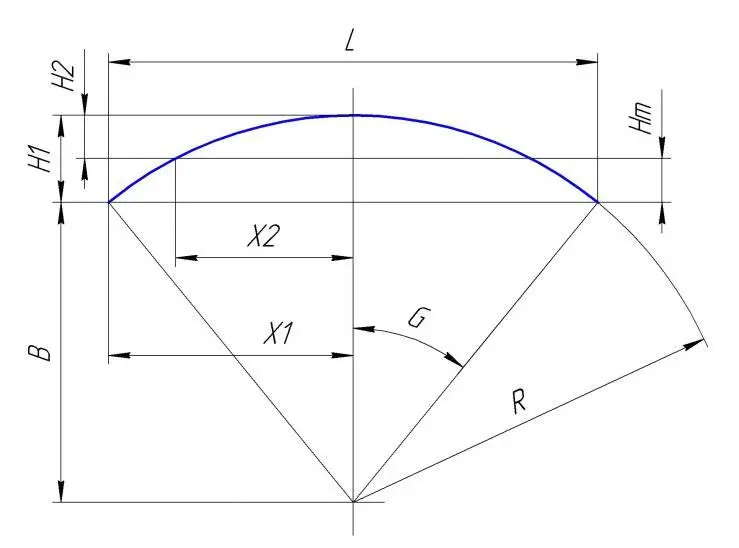
Построение части окружности методом подъема.

Построение:

Задаем максимальный размер хорды L.

Из середины максимальной хорды L строим перпендикуляр Н1.

Х1 = L / 2; В = sqrt( R*R – X1*X1); H1 = R – B;

Определили максимальную стрелу прогиба кривой H1.

Далее задаем произвольное расстояние от центральной оси Х2.

Находим стрелу прогиба Н2 = R – ( sqrt( R*R – X2*X2));

Находим высоту подъема в точке Х2: Hm = H1 – H2;

Задавая ряд текущих значений Х2 и рассчитывая соответствующие высоты подъема Hm

– получаем достаточное количество точек,

для построения радиусной кривой по точкам на этой кривой.

Контрольный расчет:

Исходные данные:

Радиус R = 10000;

Хорда максимальная заданная L = 8000;

Подъем максимальный в центре хорды = 834,8486100883201.

Задаем ряд точек:

От центра хорды до точки по оси Х-Х = 3000,0.

Величина подъема ( перпендикуляра ) = 374,2406242577763.

…

От центра хорды до точки по оси Х-Х = 2000,0.

Величина подъема ( перпендикуляра ) = 632,8075812210318.

…

От центра хорды до точки по оси Х-Х = 1000,0.

Величина подъема ( перпендикуляра ) = 784,7229811545203.

…

От центра хорды до точки по оси Х-Х = 500,0.

Величина подъема ( перпендикуляра ) = 822,3407878074104.

…

От центра хорды до точки по оси Х-Х = 0,001.

Величина подъема ( перпендикуляра ) = 834,848610088271.

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_15. ( Скачать из приложения ).

Сохраним его как Е 16. Далее на листе необходимо выполнить заголовок расчета:

Остальное аналогично предыдущему, формулы приведены выше, записи в Excelсмотрите в открытом

Листе – скачать в приложении.

Расчет геометрии треугольника

Напротив сторон треугольника лежат одноименные углы.

Рис. Геометрия треугольника.

,,,

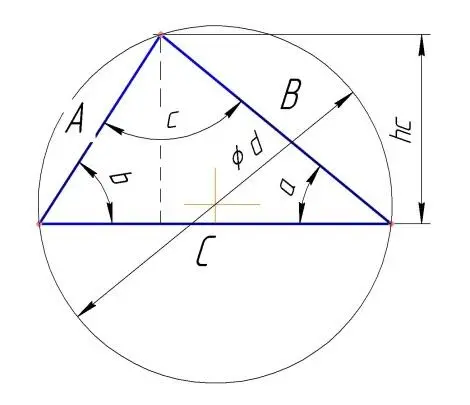
Известны три стороны треугольника

Напротив сторон треугольника лежат одноименные углы.

Сторона = a. Сторона = b. Сторона = c.

Решение:

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=аrccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=аrccos(x)… Угол В.

.cu=180-(au+bu)… Угол С.

Известны две стороны и угол между ними

Сторона = a; Сторона = b; Угол = cu..

Решение:

.с= sqrt ((a*a)+(b*b))-(2*a*b*(cos(cu)))… Сторона «с».

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=arccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=arccos(x)… Угол В.

Известны два угла и сторона между ними

Сторона = a; Угол = bu; Угол = cu;

Решение: .au=180-(bu+cu)… Угол А. .b=(a*(sin(bu)))/(sin(au))… Сторона В.

.c=(b*(sin(cu)))/(sin(bu))… Сторона С.

Добавочный расчет в алгоритм Треугольника

Решение:

R=a/(2*(sin(au))… R – Радиус описанной окружности.

.hc=b*(sin(au))… Высота из угла С.

.hb=a*( sin(cu))… Высота из угла B.

.ha=c*(sin(bu))… Высота из угла A.

S=a*ha/2.. Площадь треугольника.

Pe=a+b+c.. Периметр.

.rv=(S+S)/Pe… Радиус вписанной окружности.

…..

Контрольный расчет:

Напротив сторон треугольника лежат одноименные углы.

Сторона А = 15,77350269;

Сторона В = 14,14213562;

Сторона С = 11,54700538;

Угол А = 75; Угол В = 60; Угол С = 45..

Высота А= 10; Высота В = 11,1535507;

Высота С = 13,66025403;

Описанный радиус = 8,164965804;

Вписанный радиус = 3,804268442;

Площадь = 78,86751346;

Запись программы в Excel.

Смотри открытый и закрытый листы Е 17.. ( Скачать из приложения ).

Параметры сечения круга

Сечение – Круг

Диаметр круга d.

Контрольный расчет:

Круглое сечение: Диаметр = 80;

S=5026,548246; Jxx =2010619,298; Wxх=50265,48246.. .i=20,0…

Решение:

.s=d*d*Pii/4… Площадь круга.

.wr=Pii*d*d*d/16… Момент сопротивления радиальный.

.wx=wr/2… Момент сопротивления изгибу.