Сергей Семиков - Баллистическая теория Ритца и картина мироздания

Собственно говоря, некоторые учёные даже проговорились, что такое объяснение существовало, но было основательно забыто. Так, Г.С. Ландсберг пишет, вопреки часто приводимому в учебниках утверждению, по которому классическая теория не способна объяснить рассеяния на новой частоте, что реально и классика предсказывает смещённые компоненты излучения. Ведь, если учесть, что электроны, вылетающие из атомов под действием внутреннего фотоэффекта, обладают большими скоростями, то рассеянное ими излучение, по эффекту Доплера, обязано иметь иную длину волны [74]. Эта длина волны λ', в полном согласии с комптон-эффектом, будет зависеть от длины волны λ 0падающего излучения, от угла вылета электрона и направления рассеянного излучения. Так возникает классическая картина эффекта Комптона. Ландсберг не раскрывает подробностей этого описания и того, кто его автор. Поэтому попробуем реконструировать, восстановить эту забытую трактовку, отреставрировав классическую картину явления.

Пусть электромагнитная волна частоты f 0, падая на атом, "вырывает" из него электрон, имеющий, как показывает фотоэффект (§ 4.3), энергию mV 2/2= hf 0. Угол φ вылета электрона может оказаться любым. Падающая волна заставит этот свободно летящий со скоростью V электрон колебаться, но, в силу эффекта Доплера, — с частотой f = f 0(1+ V cosφ/ c ), отличной от f 0(Рис. 158). Вибрирующий электрон излучает вторичные волны, частота прихода f' которых, в некотором направлении θ,— отлична от частоты их испускания f . Из эффекта Доплера f' = f (1+ V cos(φ+θ)/ c )= f 0(1+ V cosφ/ c )(1+ V cos(φ+θ)/ c ). Кроме того, падающая волна заставит колебаться и излучать с частотой f 0электроны, оставшиеся в атоме. Эти две волны от атома и свободного электрона интерферируют, но правильно сложиться не могут, поскольку их частоты f 0и f' не совпадают. Во всех направлениях эти две волны сложатся беспорядочно, создавая биения, или вообще не сложатся от несинхронного прихода. И, лишь в направлении θ, для которого f 0= f'= f 0(1+ V cosφ/ c )(1+ V cos(φ+θ)/ c ), волны интерферируют за счёт равенства частот и одновременного прибытия, откуда cosφ= —cos(φ+θ), то есть φ=90°-θ/2.

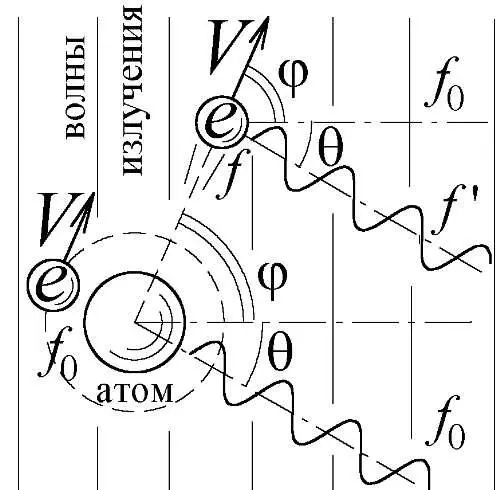
Рис. 158. Механизм комптон-эффекта: излучение f 0, "вырывая" электрон из атома, рассеивается им с частотой f'.

Подставляя значение φ, найдём, что лучи, идущие в направлении θ, имеют частоту

f' = f 0(1– V sin(θ/2)/ c )(1+ V sin(θ/2)/ c )= f 0(1–sin 2(θ/2) V 2/ c 2)

и длину волны

λ'= с / f' = λ 0+ λ 0sin 2(θ/2) V 2/ c 2.

Учтя же, что для излучения, выбившего электрон, λ 0= c / f 0=2 hc / mV 2, найдём

λ'= λ 0+ sin 2(θ/2)2 h / mc .

То есть, пришли к проверенной опытом формуле λ'—λ 0= 2λ кsin 2(θ/2), где λ к= h/mc . Также приходим к правильному соотношению углов рассеяния и отдачи, ибо если φ =90°- θ/2, то tgφ = ctg(θ/2). Это довольно точно совпадает с опытно проверенной зависимостью tgφ = ctg(θ/2)/(1+λ к/λ 0), поскольку λ к= 2,4·10 –12м обычно много меньше длины волны λ 0рентгеновского излучения, диапазон которого простирается от 10 –7до 10 –12метра. Лишь для самых жёстких рентгеновских лучей величина (1+λ к/λ 0) будет заметно отличаться от единицы. Но тогда надо, соответственно, уточнить и наш приближённый расчёт, ибо при сопоставимости λ к= h/mc и λ 0=2 ch / mV 2скорость V электрона становится сравнимой со скоростью света c , и в выражении для f' надо учесть квадратичный эффект Доплера (§ 1.20). При расчёте сделан и ряд других упрощений, конечно, не меняющих сути дела, поскольку более строгий классический анализ, учитывающий отдачу атома при испускании электрона, взаимодействие с волной обратного рассеяния и условие волнового синхронизма, даёт ту же картину эффекта Комптона.

Отметим ещё одно отличие квантовой и классической теории комптон-эффекта. В квантовой теории свет (фотон) излучается лишь в плоскости, образуемой лучом света с линией движения электрона. А в классической картине рассеянный свет излучается во всех направлениях вдоль образующих конуса, ориентированных под углом φ+θ к линии движения электрона (оси конуса), поскольку для всех этих направлений выполнено условие интерференции лучей. Однако, наиболее интенсивное излучение испускается всё же под углом θ к исходному лучу. Дело в том, что электроны, вылетающие под углом φ к оси луча и создающие излучение соответствующей длины волны λ'=λ 0+ sin 2(θ/2)2 h / mc , могут лететь не только вверх, но и вбок, и вниз, вдоль образующих конуса с углом φ и осью луча. Все эти электроны формируют свои конусы излучения, которые, складываясь, дают усреднённую картину. Касательная поверхность к этим конусам даёт каустическую поверхность, вдоль которой излучение наиболее интенсивно. Эта поверхность имеет форму конуса, с углом при вершине θ и осью, совпадающей с исходным лучом. Таким образом, хотя рассеяние происходит во всех направлениях, наиболее интенсивное излучение света длины волны λ'=λ 0+ sin 2(θ/2)2 h / mc идёт под углом θ, где θ=180°-2φ. Именно это обнаружилось в опыте. Причём, комптоновское излучение λ' действительно исходит не только в направлении θ, но и под другими углами, просто с меньшей интенсивностью. Поэтому, на спектрограммах, для данного угла θ, видно излучение не только на длине волны λ'=λ 0+ sin 2(θ/2)2 h / mc , но и на соседних длинах волн [134], чего квантовая теория объяснить не может.

Чтобы проверить, какая из теорий эффекта Комптона (квантовая или классическая) справедлива, достаточно исследовать эффект Комптона на свободных электронах, скажем летящих в вакуумных лампах или в электронно-лучевых трубках. Если эффект Комптона при этом будет наблюдаться, то справедлива квантовая теория явления. Если же он не обнаружится или будет слишком слаб, то квантовая теория ошибочна, а справедлива классическая теория, по которой лишь электроны, вылетающие из атомов, способны создавать комптон-эффект. Различить, рассеивается ли свет свободными электронами или остаточными атомами в колбе, можно по известной скорости электронов в лучевых трубках. Эта скорость внесёт известный доплеровский сдвиг в положения спектральных линий комптоновского излучения.

Было проведено много экспериментов по измерению энергий электронов в эффекте Комптона, углов испускания излучения, проверки синхронности испускания излучения и электронов [82, 134]. Все они подтвердили справедливость квантовой картины эффекта Комптона. Однако та же картина, как показано выше, должна возникать и в классическом случае, только объяснение будет совсем иным. То есть, эксперименты никоим образом не подтверждают квантовой трактовки комптон-эффекта, а, зачастую, и противоречат ей, подтверждая скорее классическую картину явления, если учесть ряд опытно выявленных особенностей эффекта Комптона.