Лидия Александровская - Сертификация сложных технических систем

Цель применения простейшего корреляционного анализа – определить и оценить линейную связь между фактором и показателем качества. При этом предполагается, что:

• связь между показателем качества и фактором случайная;

• значения показателя качества и фактора, который, возможно, влияет на него, имеют нормальное распределение вероятностей.

Типичные варианты исследования связи:

• показатель качества ремонта – себестоимость ремонта;

• затраты на ремонт – доремонтный ресурс;

• затраты на ремонт – квалификация рабочих;

• ресурс между ремонтами – год выпуска изделия;

• затраты на диагностическое оборудование – показатель качества ремонта.

Обнаружение связи или доказательство ее отсутствия между фактором X и показателем качества Y дает возможность объективно оценить проверку элементов системы качества. Например, если связь между показателем качества ремонта и квалификацией рабочих не обнаруживается, то это говорит о том, что проверка персонала этого объекта может быть ослаблена.

Для предприятия, внедряющего систему качества, использование методов корреляционного анализа дает возможность осознанно (на основе данных, а не инженерной интуиции) реали-зовывать мероприятия по управлению качеством продукции.

Например, исследование связи между метрологической характеристикой стенда для диагностирования тормозных качеств X и процентом возврата автомобилей после ремонта (по причине низкого качества тормозной системы) Y показало, что нецелесообразно управлять качеством ремонта тормозной системы за счет улучшения характеристик диагностического стенда.

Визуализацию корреляционного анализа осуществляют с использованием диаграмм рассеяния.

Порядок построения диаграммы рассеяния:

1) определяют показатель качества Y, подлежащий анализу, и параметр X, влияющий на этот показатель;

2) уточняют инженерные аспекты этой связи, т. е. физическую возможность зависимости Y (показателя качества) от параметра X;

3) определяют период наблюдений, на котором собирают данные о значениях X и соответствующих значениях Y. Таким образом, формируются два массива данных: Х 1 , Х 2 …., Х п ; Y 1 , Y 2,…, Y n. Для повышения достоверности данных целесообразно, чтобы n ≥ 20;

4) строят координатную сетку: по горизонтали – ось, на которой откладывают в соответствующем масштабе значения X; по вертикали – значения Y.

Масштабы следует подобрать таким образом, чтобы значения Х i; (i = 1, 2…., n) и значения Y i(i = 1, 2…., n) лежали в одинаковых диапазонах, т. е. точки с координатами (Х/, Y,) были заключены в некотором квадрате;

5) на координатную сетку наносят точки с координатами (Х i, Y i;) (i = 1, 2…., n), при этом возможны следующие основные варианты расположения точек (рис. 5.4):

• на рис. 5.4 а положительная корреляция (связи) между параметром X и показателем качества Y;

• на рис. 5.4 б отрицательная корреляция (связи) между параметром X и показателем качества Y;

• на рис. 5.4 в отсутствует линейная связь между параметром X и показателем Y;

• на рис. 5.4 г отсутствует линейная связь между X и Y, но есть некоторая криволинейная связь между этими характеристиками.

Следует отметить, что чем теснее линейная связь между характеристиками X и Y, тем ближе точки (Х i, Y i) концентрируются около некоторой прямой. Если между фактором X и показателем качества Y связь функциональная (т. е. не случайная), то точки (Х i, Y i) лежат строго на прямой.

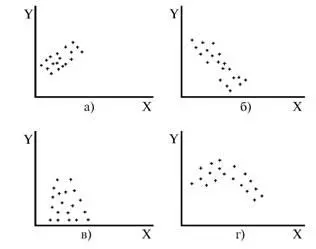
Рис. 5.4

Для объективизации этого анализа рекомендуется вычислять коэффициент корреляции r, характеризующий тесноту линейной связи:

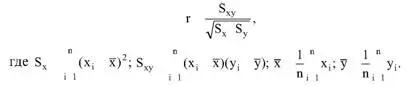
Если |г| > 1, это значит, что допущена ошибка в вычислениях, если

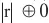
, то между Х и Y не выявлена линейная связь.

Если r близок K + 1, это значит, что между фактором Х и показателем Y существует положительная линейная связь, т. е. с увеличением параметра Х увеличивается показатель качества Y; если r близок K – 1, это значит, что между фактором Х и показателем Y существует отрицательная линейная связь, т. е. с увеличением параметра Х уменьшается показатель качества Y.

Для того чтобы убедиться в отсутствии линейной связи между рассматриваемыми факторами, что в рамках математической статистики означает проверку статистической гипотезы r = 0, используют специальный критерий, т. е. проверку условия [10]:

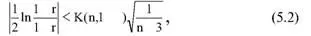
где K (n, 1 – β) – коэффициент, зависящий от объема n выборки и доверительной вероятности (0,5 <1 – β< 1).

Коэффициент K (n, 1 – β) называют квантилем распределения Стьюдента для доверительной вероятности (1 – β) и числа (n – 1) степеней свободы. Этот коэффициент определяют по таблицам [11] с двумя входами n и 1 —β.

Например, для

n = 10; β = 0,1; K (n, 1 —β) = 1,812;

n = 20; β = 0,1; K (n, 1 —β) = 1,725.

Если справедливо неравенство (5.2), то с достаточно большой вероятностью 1 – β > 0,5 можно считать, что коэффициент корреляции равен нулю, т. е. факторы линейно независимы.

Если отвергается гипотеза r = 0, то это значит, что между факторами имеется линейная связь. Для лица, проводящего аудит, это означает возможность проверки только одного фактора, информация о котором может быть получена наиболее просто в ходе проверки.

Сертификация систем качества на соответствие стандартам ИСО серии 9000 предполагает оценку (анализ) точности и стабильности производственных процессов (ПП). Такая оценка может быть выполнена с использованием индексов воспроизводимости ПП, которые получили широкое распространение в практике сертификации технологического оборудования автомобильных корпораций США и Японии.

Индексом воспроизводимости ПП (в предположении, что значение параметра ПП (детали) распределено нормально) называют характеристику С р:

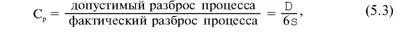
где σ – среднее квадратическое отклонение значений параметра детали от среднего значения; D – допустимый разброс (допуск).

В формуле (5.3) предполагается, что среднее значение процесса находится в середине поля допуска. Фактически С рсоотносит допуск на параметр детали с фактическим разбросом. Таким образом, если С р= 1,0, то ПП можно признать воспроизводимым в том смысле, что ПП обеспечивает установленные требования к качеству детали. Так как на практике значение у оценивается по выборке измерений параметра детали с определенными погрешностями, значение С р= 1,0 обычно не используется в качестве критического (минимально приемлемого).