Лидия Александровская - Сертификация сложных технических систем

Рассмотрим наиболее распространенный статистико-вероят-ностный подход определения объема выборки. Исходными данными для вычисления объема выборки являются предельная абсолютная Д ч или относительная д ч ошибки в оценке среднего значения показателя и предельная абсолютная ошибка D p в оценке доли признака; степень достоверности оценки, выраженная доверительной вероятностью q.

В табл. 5.6 приведены формулы для расчета объема выборки при случайном и систематическом отборе единиц продукции для оценки среднего значения показателя качества и доли единиц продукции, обладающих определенным признаком (например доля дефектных единиц).

Таблица 5.6

Примечания: 1. Принятые обозначения: 2– ожидаемое значение дисперсии измеряемой величины; V – коэффициент вариации; p – ожидаемое значение доли единиц продукции, обладающих данным признаком; t q (n 1) – квантиль распределения Стьюдента для доверительной вероятности q и числа степеней свободы n– 1.

2. При расчете n значение округляется до ближайшего целого числа.

В табл. 5.6 учтено, что измеряемая величина имеет нормальное распределение. При больших n (n ≥ 30) для упрощения расчетов целесообразно вместо значения t q (n—1) использовать квантиль нормального распределения u q .

Для больших партий расчет объема выборки без повторения можно проводить по более простым формулам для выборки с повторением.

При случайном многоступенчатом (двухступенчатом) отборе объем выборки определяют:

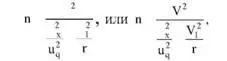
где V 1 2 , V 1 – соответственно межгрупповые дисперсия и коэффициент вариации измеряемой величины; r – число первичных упаковочных единиц, подлежащих отбору, которое зависит от количества первичных упаковочных единиц в партии R:

r………..Все 5 1/20 часть (5 %) 20

R………. 1–5 6 – 99 10 – 399 400 и более.

Предельные объемы выборки при многоступенчатом отборе:

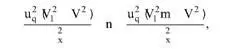
где m – число изделий в упаковочной единице.

Объем выборки при типическом (расслоенном) отборе рассчитывают по следующим формулам:

выборка без повторения выборка с повторением

где V —2 – среднее частных дисперсий по слоям.

Объем выборок из i-го слоя вычисляется по следующим формулам:

выборка, пропорциональная объему слоев

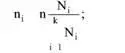
выборка с учетом изменения измеряемой величины в слоях

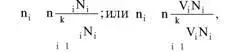
где N i– объем слоя; k – число слоев в партии; V i 2– ожидаемое значение дисперсии измеряемой величины в i-м слое; V i– ожидаемое значение коэффициента вариации в i-м слое.

Ниже приведены типовые примеры расчета объема выборки с учетом рассмотренных способов их формирования.

Пример 1. Партия проката (N = 100 листов) представлена на испытания для контроля средней толщины листа с относительной погрешностью δ = 0,1 при доверительной вероятности q = 0,9. Необходимо определить объем выборки, если известно, что коэффициент вариации толщины листа равен 0,2.

Способ представления продукции на испытания – «ряд», поэтому для формирования выборки целесообразно использовать случайный отбор. Так как выборка без повторения, то для расчета объема n выборки необходимо воспользоваться формулой из табл. 5.6, заменив значение t q (n 1) на u q :

Таким образом, для обоих типов выборок их объем примерно одинаков.

Пример 2. Партия стержней (N = 20 000 шт.), упакованная в 100 ящиков (упаковочных единиц), представлена на испытания для контроля предела усталости. Необходимо определить объем выборки для испытаний, если δ = 0,1; V = 0,3; V i= 0,05; q = 0,95.

Определим количество ящиков, подлежащих отбору из партии. Для 100 ≥ R ≤ 399 количество отобранных упаковочных единиц r = 100/20 = 5.

Для q = 0,95 по таблице квантилей найдем u q = 1,64. Тогда

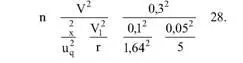
Таким образом, из пяти ящиков, случайно отобранных из партии объемом 100 ящиков, необходимо методом случайного отбора взять 28 стержней (примерно 6 шт. из каждого ящика) на испытания.

Вычислим предельные объемы выборки. Так как N = 20 000, R = = 100, то

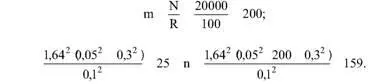
Следовательно, границы объема выборки, исходя из условий примера, составляют 25—159 единиц.

Пример 3. Учитывая условия примера 2, определить объем выборки для испытаний стержней, если вся партия продукции распределена на четыре однородные группы (слоя):

группа 1 – ящики с 1-го по 20-й (R 1= 20);

группа 2 – ящики с 21-го по 60-й (R 2= 40);

группа 3 – ящики с 61-го по 80-й (R 3= 20);

группа 4 – ящики с 81-го по 100-й (R 4= 20).

Так как партия продукции неоднородна (расслоена), то формирование выборки необходимо проводить методом расслоенного отбора с учетом наличия четырех слоев. Число упаковочных единиц (ящиков) и общий объем выборки определены в примере 2 (r = 5; n = 28).

Определим число упаковочных единиц, которые необходимо отобрать из первого слоя:

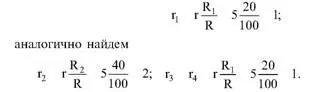
Таким образом, из первого, третьего и четвертого слоев необходимо отобрать по одному ящику, из второго слоя – два ящика.

Определим объем подвыборки, которую необходимо сформировать из продукции первой группы:

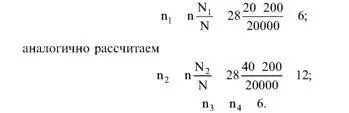
Этот факт обусловлен округлением при вычислении значений n i .

Рассмотренный пример показывает, что расслоение партии приводит к более сложной процедуре организации формирования выборки при одинаковых требованиях к точности и достоверности.

При сертификации по схеме № 7 (табл. 5.1) часто используется метод параметрического контроля. При параметрическом контроле, в частности надежности, у каждого проверяемого изделия (выборки изделий) определяется один количественный параметр х, который в партии изделий имеет определенное (нормальное, Вейбулла, гамма и т. д.) распределение.