Лидия Александровская - Сертификация сложных технических систем

В выборке объема n определяются значения параметра х 1 , …, х п , а также выборочная средняя величина

Оценка партии производится по величине х ср , для которой (как и для доли дефектных изделий в партии при непараметрическом контроле) устанавливаются два уровня: приемочный х ср aи браковочный х ср в. Соотношение между х срa и х ср вможет быть различным: в случае контроля позитивных показателей х срa > х ср в, а в случае контроля негативных показателей х срa< х срв.

Оценочный норматив (приемочное число) х срсдля среднего значения х срконтролируемого параметра назначается с учетом следующих условий:

• если х срa > х ср в, то параметр соответствует установленным требованиям в ТУ при xx cp0 и не соответствует при xx cp0 ;

• если х срa < х ср в, то параметр х ср соответствует установленным требованиям в ТУ при xx cp0 и не соответствует при x x cp0 .

В свою очередь параметрический статистический контроль может быть одноступенчатым или многоступенчатым.

Одноступенчатый контроль осуществляется по результатам одной выборки, а многоступенчатый – по результатам нескольких выборок. При этом каждой выборке в общем случае соответствует свой оценочный норматив (приемочный и браковочный уровень).

Многоступенчатые правила контроля более экономичны по сравнению с одноступенчатыми, но организация их вызывает большие трудности.

Параметрический одноступенчатый контроль. Такой контроль показателей безотказности – наработки до отказа (на отказ, между отказами) – осуществляется по выборочному среднему (5.4) значению T в соответствии со следующими условиями: приемки (соответствия контролируемого показателя заданным требованиям) TT c ; браковки (несоответствия контролируемого показателя заданным требованиям) T Т 0 , где Т 0 – оценочный норматив выборочного среднего значения наработки до отказа (на отказ, между отказами). В соответствии с этим риски поставщика и заказчика соответственно равны:

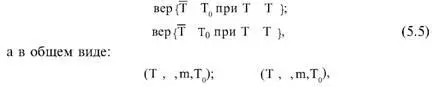
где T a , T в– уровни среднего значения наработки на отказ (до отказа, между отказами) соответственно приемочный и браковочный; v – коэффициент вариации наработки на отказ (до отказа, между отказами); m – необходимое для контроля среднего значения наработки на отказ (до отказа, между отказами) количество измерений или отказов.

План контроля (количество измерений m и оценочный норматив Т 0 ) определяется путем решения уравнений (5.5) относительно m и Т 0.

При нормальном распределении наработки до отказа (на отказ, между отказами) соотношения (5.5) принимают вид:

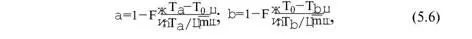
где F (·) – нормированная и центрированная функция нормального распределения.

С учетом зависимостей (5.6) требуемое количество измерений:

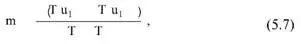
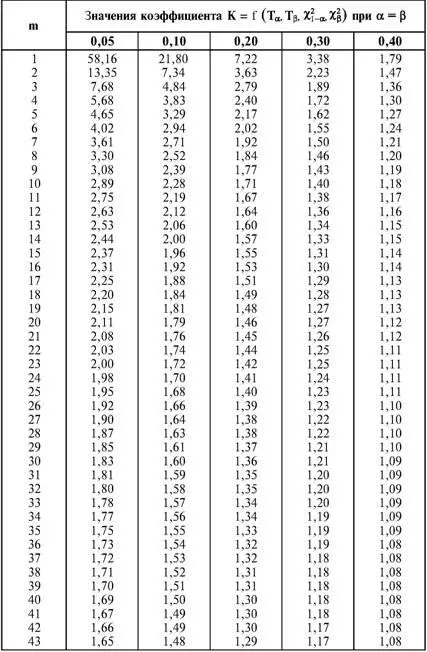
где U р – квантиль нормального распределения, отвечающая вероятности р (табл. 5.7).

При a = в = ц соотношение (5.7) можно представить в виде:

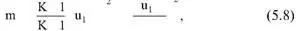
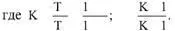
Таблица 5.7

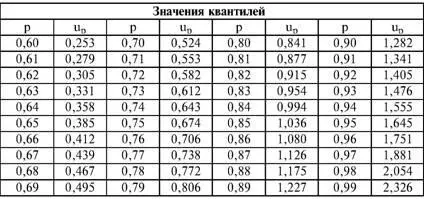
На основании зависимостей (5.6) получаются выражения для оценочного норматива:

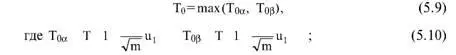
при этом m определяется из соотношений (5.7) и (5.8).

Наконец, требуемый объем (суммарная наработка в процессе испытаний):

t = mT 0 (5.11)

где m и T 0 – величины, рассчитываемые по (5.7) – (5.10).

При распределении наработки до отказа (на отказ, между отказами) по закону Вейбулла соотношения (5.5) принимают вид:

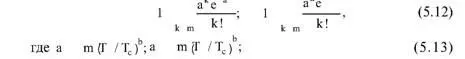
в – параметр формы распределений Вейбулла, однозначно определяющий коэффициент вариации.

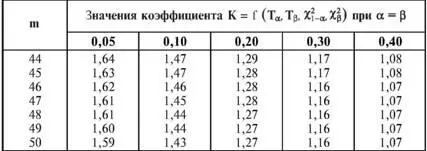
Используя соотношения (5.12), (5.13), получим (табл. 5.8):

В результате решения соотношения (5.14) относительно m (см. табл. 5.8) устанавливается необходимое для контроля Ф количество измерений наработки до отказа (на отказ, между отказами):

m = f(T a, T в, α, β, b). (5.15)

Таблица 5.8

Используя зависимости (5.12), (5.13), получим выражения для оценочного норматива:

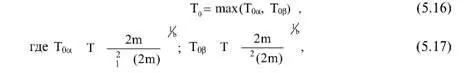
m определяется соотношениями (5.14), (5.15).

Требуемый объем (суммарная наработка в процессе испытаний), как и в случае нормального распределения, определяется выражением (5.11).

Пример 4. Известно, что наработка изделия между отказами имеет нормальное распределение с коэффициентом вариации n = 0,25. В технических условиях (ТУ) на производство изделия установлены приемочный Т а = 150 ч и браковочный Т в= 100 ч уровни средней наработки между отказами, а также соответствующие им риски α = 0,2 и в = 0,1. Требуется установить план одноступенчатого статистического контроля наработки изделия между отказами.

Для α = 0,2, β = 0,1 в табл. 5.7 найдем u 1- α= 0,841 и u 1- β= 1,282. По (5.7) определим необходимое для контроля количество измерений:

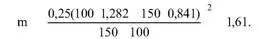
Следовательно, m = 2.

Используя зависимости (5.10), найдем

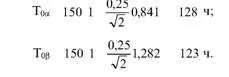
Из соотношения (5.9) определим оценочный норматив Т 0 = 128 ч. С помощью (5.11) найдем требуемую суммарную наработку изделия в процессе испытаний: t = 2256 = 128־ ч.

Таким образом, план одноступенчатого статистического контроля наработки изделия между отказами (на отказ) характеризуется величинами t = 256 ч и Т 0= 128 ч.