Вилли Лей - Ракеты и полеты в космос

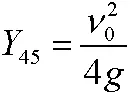
Закон Тартальи применяется и в настоящее время, но только для очень приблизительной оценки характеристик системы, так как по сути дела он ничего не объясняет.

Чем же определяется высота, достигаемая снарядом? Для простоты рассуждений остановимся вначале на особенностях полета обычного артиллерийского снаряда. Как показывают приведенные выше формулы, высота траектории снаряда при стрельбе в зенит определяется отношением скорости к силе земного притяжения. Очевидно, снаряд, покидающий ствол орудия со скоростью 300м/сек, поднимается выше снаряда, имеющего дульную скорость 150м/сек. В данном случае нас будет интересовать не столько высота подъема снарядов, сколько сам процесс их подъема и падения, а также их скорости в момент встречи с землей.

Представим себе теперь, что снаряды не испытывают сопротивления воздуха; тогда вполне законным будет утверждение, что снаряд, покинувший ствол орудия со скоростью 300м/сек при стрельбе в зенит, упадет на землю, имея скорость 300м/сек, а другой, обладавший дульной скоростью порядка 150м/сек, будет при падении иметь скорость 150м/сек. При этом оба снаряда достигнут различных высот. Если с этих же высот сбросить обычные бомбы, то их скорости при ударе о землю будут равны соответственно 300 и 150м/сек.

Это положение может быть сформулировано таким образом: скорость, необходимая для достижения определенной высоты в безвоздушном пространстве, равна скорости, развиваемой телом при падении с этой высоты. Поскольку всегда можно вычислить скорость снаряда при падении с любой заданной высоты, нетрудно определить и скорость, которую нужно сообщить ему для достижения этой высоты. Вот несколько цифр, иллюстрирующих сказанное выше:

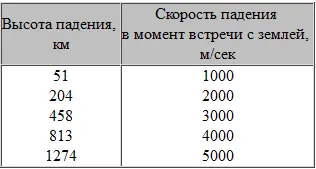
Из этих цифр видно, что высоты растут гораздо быстрее, чем соответствующие им скорости. Так, высота, указанная во второй строке, в четыре раза больше высоты, отмеченной в первой, тогда как скорости разнятся между собой только в два раза. Поэтому для определения момента отделения ракеты «ВАК-Капрал» (вторая ступень) от первой ступени («Фау-2») важна была не столько достигнутая высота, сколько полученная ракетой скорость.

Следует, однако, заметить, что в приведенных цифрах не учитывается сопротивление воздуха, а также тот факт, что сила земного тяготения уменьшается с высотой (рис. 51). Если же рассматривать все эти явления применительно к ракетам, то окажется, что для них вовсе не важно, на какой высоте двигатель прекращает работу. Ниже приводятся данные, показывающие зависимость высоты подъема от скорости, для ракет с ускорением 3g; при этом учтено только изменение силы тяжести с высотой, а сопротивление воздуха в расчет не принято.

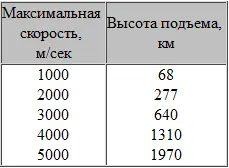
Если сравнить обе группы приведенных данных, то можно сделать один очень интересный вывод, а именно: при падении тела с бесконечной высоты его скорость при ударе о землю не может быть бесконечной. Эта скорость вполне поддается вычислению и составляет 11,2км/сек.

Таким образом, при отсутствии сопротивления воздуха пушка, снаряд которой имеет дульную скорость 11,2км/сек, могла бы выстрелить в бесконечность. Ее снаряд вышел бы из сферы земного притяжения. Поэтому скорость 11,2км/сек называют «скоростью убегания», или «второй космической скоростью».

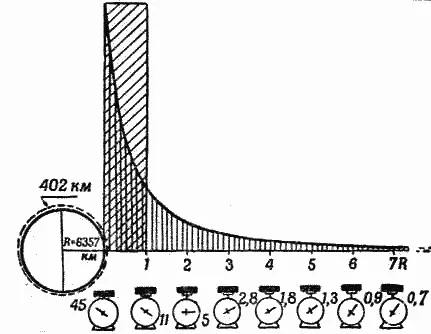
Рис. 51. Гравитационное поле Земли.

Относительная сила поля показана кривой и группой пружинных весов (нижняя часть рисунка), на которых взвешиваются одинаковые металлические гири. Гиря, весящая на поверхности Земли 45кг, на расстоянии в половину земного диаметра будет весить только 11кг, на расстоянии в один диаметр—5кг и т. д. Общая площадь, ограниченная кривой, равна прямоугольнику, то есть действительное гравитационное поле равно полю, имеющему напряженность, отмечаемую у поверхности Земли, и простирающемуся на высоту одного земного радиуса

Рассмотрим в качестве иллюстрации техническую идею романа Жюля Верна «Из пушки на Луну». Она довольно проста: огромная пушка стреляет в зенит снарядом с дульной скоростью порядка 11,2км/сек. По мере того как снаряд набирает высоту, скорость его непрерывно уменьшается под действием силы земного тяготения. В первое время эта скорость будет уменьшаться на 9,75м/сек, потом на 9,4м/сек, на 9,14м/сек и т. д., становясь все меньше и меньше с каждой минутой.

Несмотря на то, что степень уменьшения скорости под воздействием силы земного тяготения непрерывно убывает, снаряд Жюля Верна израсходует весь запас скорости фактически только через 300 000 секунд полета. Но к этому времени он окажется- на таком расстоянии, где гравитационные поля Земли и Луны уравновешивают друг друга. Если в этой точке снаряду не хватит запаса скорости всего лишь в несколько см/сек., он упадет обратно на Землю. Но при наличии даже такого запаса скорости он начнет падать в направлении Луны. Еще через 50000 секунд он разобьется о поверхность Луны при скорости падения около 3,2км/сек, затратив на все путешествие 97 часов 13 минут.

Вычислив заранее продолжительность этого полета, Жюль Верн нацелил свою пушку в расчетную точку встречи, то есть туда, где Луна должна была появиться через четыре дня после команды «Огонь!».

Несмотря на то, что исходные данные в романе очень близки к истине, технические детали осуществления грандиозного проекта либо недоработаны, либо весьма неопределенны. Так, в ствол гигантской «пушки», отлитой прямо в земле, закладывается произвольное количество пироксилина (181000кг), причем автор полагает, что этого количества пироксилина будет достаточно для обеспечения снаряду дульной скорости 16км/сек. В другом месте романа утверждается, что для снаряда с такой высокой начальной скоростью сопротивление воздуха не будет иметь значения, потому что, мол, на преодоление атмосферы уйдет всего лишь несколько секунд.

Последнее замечание аналогично утверждению, что броневая плита толщиной 1м не сможет задержать 16-дюймовый снаряд, так как расстояние в 1м он преодолевает за 0,001 секунды.

Если бы эксперимент с «пушкой» Жюля Верна был осуществлен на практике, то исследователи, вероятно, пришли бы в величайшее удивление, так как снаряд упал бы в 30м от дула «пушки», поднявшись примерно на такую же высоту. При этом снаряд был бы сплющен, а часть его могла бы даже испариться. Дело в том, что Жюль Берн забыл о сопротивлении воздуха, встречаемом снарядом в 210-м стволе пушки. После выстрела снаряд оказался бы между двумя очень горячими и чрезвычайно мощными поршнями, то есть между бешено расширяющимися газами пироксилина снизу и столбом нагретого при сжатии воздуха сверху. Разумеется, все пассажиры такого снаряда были бы раздавлены огромной силой ускорения снаряда.