Нина Рябинина - Технология редакционно-издательского процесса

2. Формула должна иметь хороший графический рисунок. Плохо воспринимаются, например, цифры в середине сомножителей (их лучше ставить спереди), сложные показатели степени и индексы, многоступенчатые индексы, сложные формулы, приведенные к компактному виду.

Особой разновидностью искажений графики, еще больше ухудшающих «внешний вид» формулы, являются нарушения пра–вил набора. Желая упростить его, иногда смещают верхние индексы относительно нижних (K ав ткм). Точки в индексах часто оказываются не на месте и выглядят знаком умножения (Д Б . П ). Запятые после формул неопытные наборщики набирают в индексах (А =ВС к ). Не соблюдаются правила выбора кегля для подключек, в результате чего формула и экспликация становятся не похожими друг на друга. Если в индексах встречаются буквы разных алфавитов, часто они плохо выравниваются («пляшут»). Знак деления «косая черта» по высоте часто ниже (меньше кегль) делимого и делителя.

Из сказанного можно сформулировать рекомендации по улуч–шению воспроизводимости и графики формул.

Что касается главного условия хорошей воспринимаемости формул – облегчения их понимания и запоминания, – необходимо учитывать следующие рекомендации:

– при прочих равных условиях русские символы, являющиеся первой буквой зашифрованного слова, воспринимаются, т.е. по–нимаются и запоминаются, лучше, чем латинские или греческие;

– в качестве символов нежелательно использовать аббревиатуры, так как они воспринимаются как произведение;

– индекс по возможности должен яснее отражать зашифрованное в нем слово или словосочетание;

—легко понимается и запоминается формула, в которой на–глядно отражена зависимость результата вычисления от характера изменения параметров.

Единицы физических величин следует помещать только после подстановки в формулу числовых значений величин и проведения промежуточных вычислений – при получении конечного результа–та. Например:

неправильно:

с = КТм/с = 1,4 · 290 · 300 м/с = 350 м/с;

правильно:

с = КТ = 1,4 · 290 · 300 = 350 м/с.

Математические знаки определяют как символы, служащие для записи математических понятий, предложений и вычислений. Так, «отношение длины окружности к длине ее диаметра» записы–вается в виде знака щ.

Математические знаки подразделяются на три группы:

1) знаки математических объектов (точки, прямые, плоскости) обычно обозначаются соответственно буквами (А, В, С…; а, b, с…; α, β, γ ... );

2) знаки операций сложения (+) и вычитания (-); возведения в степень а 2 , а 3 и т.д.; корня V; знаки тригонометрических функ–ций log, sin, cos, tg и др.; факториала !; дифференциала и интеграла dx, ddx,…, ∫ydx, модуля | х |;

3) знаки отношений (= – равенство, > – больше, < – меньше, || – параллельность, ⊥ – перпендикулярность, ≡ – тождествен–ность, ≅ – приблизительное равенство).

Все эти знаки, кроме знаков объектов, применяются только в формулах, использовать их в тексте вместо слов соответствующего значения запрещается. Знаки объектов в тексте могут применяться со словами: в точке А, на плоскости а, из угла х.

Часто после формулы идет экспликация – расшифровка входя–щих в формулу символов. Элементы ее располагаются в той после–довательности, в которой условные обозначения прочитываются в формуле. Одни и те же буквы с разными индексами рекоменду–ется группировать вместе. При расшифровке дробных формульных выражений сначала поясняют буквенные обозначения числителя, а затем знаменателя.

Если необходимо расшифровать значение символа, стоящего в левой части уравнения, это рекомендуется делать в предшествую–щей формуле части предложения. К сожалению, эта рекомендация не всегда выполняется.

Приведем примеры из журнала «Военно-экономический вест–ник» (2002. № 12).

Расчет затрат на перевозки вооружения и техники осуществляются по формуле

З п.в.т = В п.в.т × С п.в.т × Д п (29)

где З п.в.т – затраты на перевозки однотипного вооружения и техники, руб.; В п.в.т – количество перевозимого вооружения (техники) данного типа, ед.; С п.в.т – стоимость перевозки 1 единицы вооружения (техники) на 1 км в руб.; Д п – дальность перевозки вооружения (техники), км.

Расчет производится по каждому виду вооружения (техники) в от–дельности.

Кроме того, для крепления перевозимого вооружения и техники на платформе используется крепежный материал – проволока, гвозди, скобы, брус деревянный или специальные крепежные приспособле–ния. Для их приобретения также требуются денежные средства. Расчет затрат на приобретение крепежного материала производится по формуле

З к.м= В п.в.т × Ц к.к.м, (30)

где З к.м– затраты на приобретение крепежного материала, руб.; В п.в.т– количество перевозимого вооружения и техники, ед.; Ц к.к.м– цена 1 комплекта крепежного материала (на единицу техники), руб.

Затраты на приобретение крепежного материала (крепежных при–способлений) рассчитываются отдельно только в том случае, если они не входят в расценки на перевозки вооружения и техники.

Затраты на перевозки личного состава на учениях различными ви–дами транспорта определяются по формуле

З п.л.с= В л.с × С п.ч × Д п, (31)

где З п.л.с– затраты на перевозки личного состава на конкретном виде транспорта, руб.; В л.с– количество перевозимого личного состава на конкретном виде транспорта, ед.; С п.ч– стоимость перевозки одного человека на 1 км конкретным видом транспорта, руб.; Д п– дальность перевозки личного состава, км.

И в первой, и во второй, и в третьей формулах символ, стоя–щий в левой части уравнений, следовало бы расшифровать в пред–шествующем формуле тексте. Символ В везде обозначает количе–ство перевозимого вооружения или личного состава, ед. Символ С – стоимость перевозки 1 человека, 1 единицы вооружения на 1 км; Д – дальность перевозки вооружения, личного состава, км. Следовало бы дать расшифровку символов один раз, не повторяя ее после каждой формулы.

После формулы перед экспликацией ставят запятую, а экспли–кация начинается словом где, за ним следуют обозначение первой величины и ее расшифровка и т.д. В конце каждой расшифровки рекомендуется ставить точку с запятой, в конце последней – точ–ку. Обозначения единиц физических величин в расшифровках от–деляют от текста запятой. Например:

Индуктивность многослойной катушки определяется по формуле

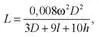
где ω – число витков; D – средний диаметр намотки, мм; l – длина намотки, мм; h – высота намотки, мм.

Экспликация к формулам не стандартна. В научной литературе можно найти различные ее варианты – от самого простого до сложного, относящегося к одной формуле и к нескольким. Если формулы в предложении разделены текстом, общую экспликацию к ним лучше выделить в самостоятельное предложение. Например: