Нина Рябинина - Технология редакционно-издательского процесса

Косой крест (×) как знак умножения применяется в формулах:

– при указании размеров: площадь комнаты 4 × 3 м;

– при записи векторного произведения векторов: а × b;

– при переносе формулы с одной строки на другую на знаке умножения.

Перенос формул. Если приводимая в рукописи формула на–столько длинна, что не помещается в одной строке на странице издания (без переноса), обычно требуют, чтобы автор наметил возможные места переноса. Предпочтительнее перенос делать в первую очередь на знаках математических соотношений: = ≠ , ≈, ≡,≤, ≥, >, <, >> и т.д.

Если на этих знаках разделить формулу на строки не удается, ее следует делить на знаках операций + или —. Менее желательно, хотя и допустимо, деление формул на строки на знаках ± и умно–жения. Не принято делить строку на знаке деления (две точки). Если формулу делят на знаке умножения, его показывают не точ–кой, а косым крестом (×).

Особенно внимательно подходят к вопросу о переносе уравне–ний, правая или левая часть которых представлена в виде дробей с длинными числителями и знаменателями или с громоздкими подкоренными выражениями. Такие уравнения необходимо пре–образовывать, приводя их к виду, удобному для переноса.

Дроби с длинным числителем и коротким знаменателем целе–сообразно представлять так, чтобы числитель был записан в виде многочлена в скобках, а единица, деленная на знаменатель, вы–несена за скобки. Например, уравнение

легко приводится к виду

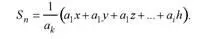
При коротком числителе и длинном знаменателе рекомендуется заменять отдельные сложные элементы упрощенными обозначе–ниями. Например: вместо

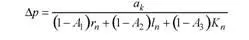
надо

Если в формулу входит дробь с длинным числителем и длин–ным знаменателем, то для переноса либо используют оба реко–мендованных приема преобразования, либо заменяют горизон–тальную дробную черту знаком деления (две точки). В последнем случае формула будет иметь вид

( a 1 x + a 2 y + ... + a i h ) : ( b 1 x + b 2 y + ... + b ih ).

Подкоренное выражение рекомендуется преобразовать путем возведения его в степень 1/и. Например, формулу

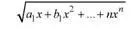
можно записать так:

( a 1 x + b 1 x 2+ ... + nx n ) 1/2.

Знаки, на которых делают перенос, ставят два раза: в конце первой строки и в начале перенесенной части. Например:

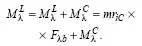
Если формулу прерывают на отточии, его также повторяют в начале следующей строки. Если знак равенства стоит перед зна–ком минус, перенос делают на знаке равенства. Если формула имеет в своем составе несколько выражений в скобках, перенос рекомендуется делать на знаке + или –, стоящем перед скобками.

Несмотря на все старания редакторов и корректоров, погреш–ности в тексте с формулами все же остаются. Типичная ошибка при переносе формул – отрыв аргумента от функции. Например:

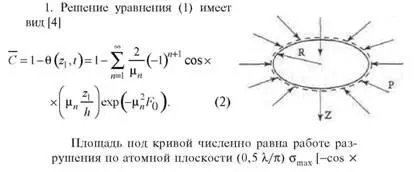
Конечно, нельзя требовать от наборщика, чтобы он дифферен–цированно оценивал запись типа f(x – y): без контекста невозможно сказать, что она означает: произведение двух функций f и (х – у) или зависимость функции f от аргумента (х – у). Однако известно, что тригонометрические функции без аргумента не имеют смысла, поэтому без них не употребляются. И помещать знак умножения между функцией и ее аргументом – грубейшая ошибка.

В приведенном примере редактор не мог предусмотреть допу–щенных ошибок. В первом случае перенос формулы вызван недо–смотром наборщика при разбивке ее на две строки, во втором формула была в самом тексте, и предвидеть ее перенос в этом месте при редактировании было практически невозможно. Но в верстке редактор обязан был исправить эту ошибку.

Емкость печатного листа с формулами в 2—3 раза меньше емкости печатного листа текста, что увеличивает себестоимость издания. Издательская практика располагает рациональными приемами по–дачи формул, дающими ощутимый экономический эффект. Фор–мулы, как правило, набирают в красную строку с отбивкой сверху и снизу. Это ведет к увеличению расхода бумаги, удорожанию на–бора и монтажа формул.

Выключка формул посередине формата целесообразна в двух случаях: а) формула нуждается в акценте; б) из-за сложности и громоздкости формула не может быть набрана вместе с текстом. Формулы, на которые необходимо обратить внимание, как прави–ло, нумеруются. Однако часто формулы выключают без всякой необходимости.

Например, текст

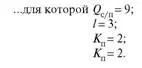
вполне можно разместить в одной строке.

Существенного уплотнения набора можно добиться и тогда, когда этому, казалось бы, препятствует нумерация формул. На–пример:

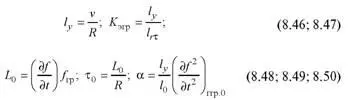
При таком расположении формул найти ее номер не составляет труда.

Иногда авторы помещают одну под другой несколько однотип–ных формул, каждой давая номер.

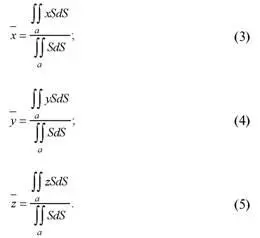
В подобном случае все формулы можно поместить в одной строке под одним номером:

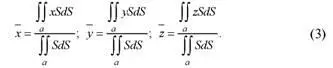
Изменение ссылок на них не вызывает затруднений. Если, на–пример, нужно сослаться на формулу для выражения координаты, можно написать: «по второй из формул (3)».

Методы преобразования, заложенные в природе самой форму–лы, позволяют практически любую формулу любой сложности представить в виде, удобном для набора. Простейшая дробь

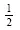
оказывается неудобной для набора. Но ее можно записать или через косую черту 1/2, или десятичной дробью 0,5, или в виде степени 2 -1 . Все варианты равноправны, однако наибольшее распростра–нение получил первый.