Нина Рябинина - Технология редакционно-издательского процесса

Сложнее расставлять знаки препинания в предложении с фор–мулой, выделенной в отдельную строку. Особенно вызывает спор постановка знака перед формулой.

Возьмем самый общий случай, т.е. формульный текст следующе–го типа (рис. 2), и рассмотрим знаки препинания перед формулой, между несколькими формулами, после формулы и в послефор-мульном тексте.

Рис. 2. Общий случай формульного текта

Перед формулой может не быть никакого знака, могут стоять за–пятая, двоеточие. После текста, предшествующего формуле, обычно никаких знаков препинания не ставят, если формула представляет собой член предложения, который по правилам пунктуации не должен отделяться от предшествующих слов знаками препинания. Например:

Эффективность канала мы характеризуем величиной

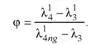
Запятая перед формулой обычно ставится, если предформульный текст оканчивается вводным словом. Например: Но для решеток ВНА всегда α1 = 0, следовательно,

d 2 = −θ − i p+ G p= f (θ, t ∗) и G p= f (θ, t ∗) ≠ f ( d 2).

Запятая ставится также тогда, когда перед формулой заканчива–ются придаточное предложение, причастный или деепричастный оборот.

Теперь, если Р ех и е е оба равны нулю,

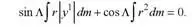
Из формулы (36) получим, вводя коэффициенты расхода,

Самым спорным вопросом пунктуации в тексте с формулами является постановка двоеточия перед формулой. Двоеточие в рус–ском языке ставится перед однородными членами предложения после обобщающего слова, в бессоюзных сложных предложениях, при прямой речи и использовании цитат.

Перед формулой двоеточие может быть поставлено в следующих случаях.

1. Если перед несколькими формулами есть обобщающее сло–во; при отсутствии его двоеточие перед несколькими формулами следует ставить только в тех случаях, когда нужно предупредить читателя, что далее следует перечисление нескольких формул:

Применяя теорему наложения к уравнению (8.32), получим два вида интеграла свертки, или интеграла Дюамеля:

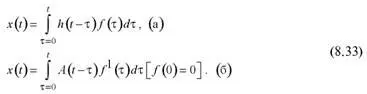
Из уравнения (3) получим:

2. Если формульный текст можно рассматривать как бессоюз–ное сложное предложение, в котором формула, являясь второй частью, либо разъясняет смысл первой части (возможна мыслен–ная постановка слов а именно), либо содержит причину или обо–снование того, о чем говорится в первой части (возможна мыслен–ная постановка слов потому что, так как, поскольку).

Подставим выражение (3.57) в формулу для B 0 :

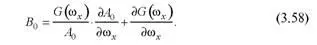
Мы предполагаем, что С he , есть линейная функция:

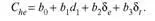
Между формулами принято ставить точку с запятой или запя–тую в зависимости от того, какой знак проводится по всей работе.

В системах уравнений, объединенных парантезами, знаки пре–пинания можно не ставить, рассматривая систему как единый член предложения. Например: Из системы уравнений

можно определить значения постоянных коэффициентов.

Если системой уравнений заканчивается предложение или вслед за системой приводят экспликацию, такую систему рас–сматривают как перечисление формул и отделяют их друг от друга соответствующим знаком.

Иногда две формулы соединяются союзом или. Союз или упо–требляется в русском языке в двух значениях: как разделительный и как уточняющий. Разделительный союз или (одиночный или по–вторяющийся) указывает на необходимость выбора одного из по–нятий, которые выражаются однородными членами и исключают или заменяют друг друга. Перед одиночным разделительным сою–зом или запятая не ставится.

Если союз или имеет уточняющее значение, то запятая перед одиночным союзом ставится обязательно.

Редактору необходимо определить, в каком значении автор употребил союз или между формулами. Иногда нетрудно понять, что вторая формула, присоединенная союзом или, это просто пре–образованная первая формула, и запятая нужна. Так бывает в слу–чаях, когда вместо буквенных обозначений в ту же формулу под–ставляют их числовые значения. Например:

…применим уравнение (2) и после перегруппировки членов полу–чим

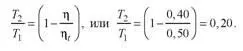
Такие конструкции встречаются редко. Поэтому для проверки идентичности формул редактору приходится делать некоторые математические преобразования. Они элементарны (не выходят за пределы курса средней школы) и под силу любому редактору. Рассмотрим несколько примеров.

Из курса тригонометрии известно, что 2 sin θ2 cos θ2 – это фор–мула двойного угла синуса, т.е. 2 sin θ2 cos θ2 = sin 2θ2. Следователь–но, во второй формуле 2 sin θ2 cos θ2 заменено на sin 2θ2, значит, формулы идентичны и запятую нужно ставить обязательно.

Здесь правая часть первого уравнения сокращена на cos θ2. Формулы тоже идентичны, и запятая нужна.

Постановка запятой перед союзом или в данном случае не тре–бует пояснений.

В этой связи рассмотрим рекомендации для «обработки мате–матического текста, в частности формул, позволяющей без ущер–ба для содержания и усвоения материала добиться либо сокраще–ния числа формул, либо упрощения их написания, уменьшения площади, занимаемой ими в книге».

Рекомендация следующая.

Иногда бывает необходимо выделить целый ряд формул, по–следовательно получающихся в результате математических преоб–разований, характер которых ясен читателю без дополнительных пояснений. Как правило, все такие формулы выключают посере–дине формата полосы, а сами формулы соединяют словами или, т.е., откуда и т.п., каждая из которых занимает отдельную строку. Однако тот же текст займет гораздо меньшую площадь, если убрать соединительные слова (заменить их точкой с запятой) и располо–жить формулы более компактно.