Вадим Грибунин - Цифровая стеганография

А7. (Barni [23]). Этот алгоритм является улучшением предыдущего, и в нем также выполняется ДКП всего изображения. В нем детектору уже не требуется исходного изображения, то есть схема слепая. Для встраивания ЦВЗ используются не наибольшие АС-коэффициенты, а средние по величине. В качестве ЦВЗ выступает произвольная строка бит.

Выбранные коэффициенты модифицируются следующим образом:

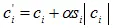. (5.30)

Далее выполняется обратное ДКП, и производится дополнительный шаг обработки: исходное и модифицированное изображения складываются с весовыми коэффициентами:

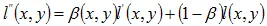. (5.31)

Здесь β ≈ 1 для текстурированных областей (в которых человеческий глаз мало чувствителен к добавленному шуму) и β ≈ 0 в однородных областях. Значение β находится не для каждого пиксела в отдельности, а для неперекрывающихся блоков фиксированного размера. Например, в качестве β целесообразно использовать нормализованную дисперсию блоков.

В детекторе ЦВЗ вычисляется корреляция между модифицированным изображением и ЦВЗ, .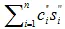

А8. (Fridrich [24]). Алгоритм является композицией двух алгоритмов: в одном данные встраиваются в низкочастотные, в другом — в среднечастотные коэффициенты ДКП. Как показали авторы, каскадное применение двух различных алгоритмов приводит к хорошим результатам в отношении робастности. Это объясняется видимо тем, что недостатки одного алгоритма компенсируются достоинствами другого. Также, как и в двух предыдущих алгоритмах, здесь осуществляется ДКП всего изображения. Исходный сигнал детектору ЦВЗ не требуется.

Перед встраиванием ЦВЗ в НЧ коэффициенты изображение преобразуется в сигнал с нулевым средним и определенной дисперсией так, чтобы абсолютные значения коэффициентов ДКП находились в диапазоне (200,250). Авторы использовали для этой цели следующее преобразование

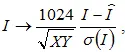, (5.32)

где σ( I ) — стандартное отклонение, — среднее значение яркости. ЦВЗ представляет собой последовательность чисел {-1;1}.

Далее строится индексная функция ind(t) на основе последовательности вещественных чисел, определяемой выражением

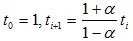, (5.33)

где параметр 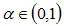. Индексная функция

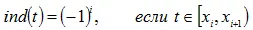. (5.34)

Таким образом, для каждого вещественного числа t можно определить его индекс. Этот индекс изменится только в том случае, если к числу t прибавить/отнять число, превосходящее значение αt . На рис. 5.12 показан вид функции ind(t) для α = 0.1.

Для внедрения бита ЦВЗ s i в коэффициент c j последний изменяется не менее, чем на 100α процентов так, чтобы 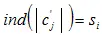. Если значение коэффициента мало (меньше 1), то в него информация не встраивается.

В детекторе используются все коэффициенты, а не только наибольшие. Это связано с тем, что позиции наибольших коэффициентов ДКП исходного и модифицированного изображений могут не совпадать. Вычисляется коэффициент корреляции, взвешиваемый с энергией коэффициентов

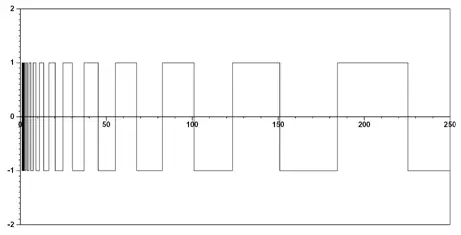
Рис. 5.12. Индексная функция ind(c)

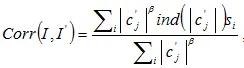, (5.35)

где параметр β определяет важность взвешивания: если он равен нулю, то взвешивания не происходит. Авторы рекомендуют использовать .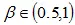

Если изображение было модифицировано, то стандартное отклонение σ( I' ) отлично от σ( I ). При знании s = σ( I )/σ( I' ) можно было бы уточнить выражение для коэффициента корреляции:

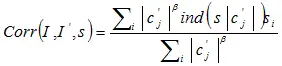. (5.36)

Однако, как было указано, исходное изображение отсутствует у детектора. Поэтому значение s выбирается так, чтобы оно максимизировало значение коэффициента корреляции:

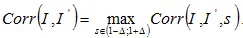. (5.37)

В среднечастотные коэффициенты ДКП информация встраивается путем умножения преобразованного значения ЦВЗ на параметр α и сложения результата со значением коэффициента. Предварительное кодирование ЦВЗ выполняется по следующему алгоритму.

Вход алгоритма: сообщение длины M , состоящее из символов .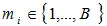

Выход алгоритма: ЦВЗ длины N , состоящий из вещественных чисел s i .

Для кодирования символа m i генерируется N+B+1 чисел псевдослучайной последовательности 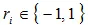. Эту последовательность будем называть i -м случайным вектором.

Первые m i чисел этого вектора пропускаются, а следующие N чисел образуют вектор V i , используемый при дальнейшем суммировании.

Для каждого символа сообщения генерируются статистически независимые различные случайные вектора.

В качестве ЦВЗ используется сумма векторов V i . Если M достаточно велико, то ЦВЗ будет иметь гауссовское распределение. i -й символ исходного сообщения может быть получен после вычисления взаимной корреляции ЦВЗ с i -м случайным вектором. N имеет величину от 1000 до 10000.

Встраивание ЦВЗ в небольшие по размеру блоки имеет то преимущество, что при этом существует возможность адаптации к локальной яркости и гладкости изображения. Однако при достаточной энергии ЦВЗ появляется артефакт блочности, также как и при высокой степени сжатия в стандарте JPEG. Перекрывающееся ортогональное преобразование (ПОП) изначально было предложено для преодоления недостатка ДКП при сжатии изображений. В работе [25] предложено его использование для внедрения информации. Чтобы увеличить робастность алгоритма вложения, авторы предложили дополнительно встраивать некий шаблон, причем этот процесс происходит в области преобразования Фурье. В результате получился алгоритм, достаточно стойкий ко многим атакам.