Чарльз Петцольд - Код. Тайный язык информатики

Л × Х = Л.

Выражение Л × Х = Х было бы неправильным, поскольку множество всех смертных существ включает кошек, собак и деревья.

Выражение «Сократ — человек» означает, что пересечение множества Сократов (очень небольшого множества) и множества всех людей (гораздо более крупного множества) представляет множество Сократов:

С × Л = С.

Поскольку из первого уравнения известно, что Л равно Л × Х, можем подставить это выражение во второе:

С × (Л × Х) = С.

Согласно ассоциативному закону это равнозначно выражению:

(С × Л) × Х = С.

Однако мы уже знаем, что С × Л равно С, поэтому можем упростить выражение, используя эту подстановку:

С × Х = С.

Теперь мы закончили. Эта формула указывает, что пересечение множества Сократов и множества всех смертных существ есть С, а это значит, что Сократ смертен. Если бы вместо этого оказалось, что С × Х равно 0, мы бы пришли к выводу, что Сократ не был смертным. Если бы мы обнаружили, что С × Х равно Х, то вывод заключался бы в том, что Сократ является единственным смертным существом, а все остальные бессмертны.

Использование булевой алгебры может показаться излишним для доказательства очевидного факта (особенно учитывая то, что Сократ доказал собственную смертность 2400 лет назад), однако ее можно использовать для того, чтобы определить, удовлетворяет ли что-то определенному набору критериев. Возможно, однажды вы зайдете в зоомагазин и скажете продавцу: «Мне нужен стерилизованный кот белого или рыжего окраса, или стерилизованная кошка любого окраса, кроме белого, или я возьму любую из имеющихся у вас черных кошек». И продавец скажет, что вам нужна кошка из множества, описываемого следующим выражением:

(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.

Верно? И вы ответите: «Да! Точно!»

Проверяя, правильно ли продавец вас понял, можно отказаться от понятий объединения и пересечения, вместо них использовать слова ИЛИ и И. Я пишу эти слова заглавными буквами, потому что они не только соответствуют понятиям в обычном языке, но и могут представлять собой операции в булевой алгебре. Когда вы формируете объединение двух множеств, вы фактически берете элементы из первого ИЛИ второго множества. А когда вы формируете пересечение, то берете только те элементы, которые одновременно принадлежат первому И второму множествам. Кроме того, вы можете использовать слово НЕ везде, где встречается символ 1, за которым следует знак «минус». Таким образом:

символ «+» (ранее обозначавший объединение) теперь означает ИЛИ;

символ «×» (ранее обозначавший пересечение) теперь означает И;

выражение «1 –» (ранее обозначавшее множество всех элементов, за исключением чего-то) теперь означает НЕ.

Именно поэтому приведенное выше выражение также может быть записано:

(М И С И (Б ИЛИ Р)) ИЛИ (Ж И С И (НЕ Б)) ИЛИ Ч.

Как видите, это соответствует тому, что вы сказали. Обратите внимание, как скобки уточняют ваши пожелания. Вам нужна кошка, принадлежащая одному из трех множеств.

(М И С И (Б ИЛИ Р))

ИЛИ

(Ж И С И (НЕ Б))

ИЛИ

Ч

С помощью этой формулы продавец может выполнить то, что называется проверкой условия. Незаметно мы перешли к несколько иной форме булевой алгебры, в которой буквы не обозначают множества. Вместо этого буквы теперь могут соответствовать числам. Однако буквам может быть присвоено только значение 0 или 1. Число 1 означает «да», «истина», данная конкретная кошка удовлетворяет этим критериям, число 0 — «нет», «ложь», данная кошка не удовлетворяет этим критериям.

Сначала продавец приносит нестерилизованного рыжего кота. Вот выражение, описывающее множество приемлемых кошек:

(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.

Вот как оно выглядит после подстановки значений 0 и 1:

(1 × 0 × (0 + 1)) + (0 × 0 × (1 – 0)) + 0.

Обратите внимание: единственными символами, которым было присвоено значение 1, являются М и Р, поскольку речь идет о рыжем коте.

Теперь нужно упростить данное выражение. Если оно упрощается до 1, то кошка удовлетворяет вашим критериям; если оно упрощается до 0, то кошка критериям не удовлетворяет. Имейте в виду, что в процессе упрощения выражения мы на самом деле ничего не складываем и не умножаем, хотя обычно можем сделать вид, что выполняем эти операции. Большинство тех же правил применяются тогда, когда символ «+» означает ИЛИ, а символ «×» — И. Иногда в современных текстах для обозначения И и ИЛИ используются символы «∧» и «∨» вместо «×» и «+». Однако именно здесь символы «+» и «×», вероятно, имеют наибольший смысл.

Когда символ «×» означает И, возможны результаты:

0 × 0 = 0;

0 × 1 = 0;

1 × 0 = 0;

1 × 1 = 1.

Другими словами, результат равен 1 только в том случае, если левый И правый операнды равны 1. Эта операция соответствует обычному умножению и называется конъюнкцией , и ее можно описать с помощью небольшой таблицы, аналогичной таблицам сложения и умножения, приведенным в главе 8.

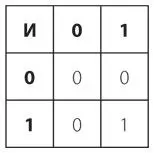
Когда символ «+» означает ИЛИ, возможны следующие результаты.

0 + 0 = 0;

0 + 1 = 1;

1 + 0 = 1;

1 + 1 = 1.

Результат равен 1, если левый ИЛИ правый операнд равен 1. Исход этой операции похож на результаты обычного сложения, за исключением того, что в данном случае 1 + 1 равно 1. Результаты операции ИЛИ, которая называется дизъюнкцией, можно представить в виде другой таблицы.

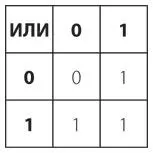
Мы готовы использовать эти таблицы для вычисления:

(1 × 0 × 1) + (0 × 0 × 1) + 0 = 0 + 0 + 0 = 0.

Результат 0 — «нет», «ложь», этот котенок не подходит.

Затем продавец приносит стерилизованную белую кошку. Исходное выражение выглядело так:

(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.

Снова подставим в него значения 0 и 1:

(0 × 1 × (1 + 0)) + (1 × 1 × (1 – 1)) + 0.

И упростим его:

(0 × 1 × 1) + (1 × 1 × 0) + 0 = 0 + 0 + 0 = 0.

Еще один несчастный котенок отвергнут.

Затем продавец приносит стерилизованную серую кошку. (Серый соответствует критерию «другой окрас», то есть не белый, не черный и не рыжий.) Вот соответствующее выражение:

(0 × 1 × (0 + 0)) + (1 × 1 × (1 – 0)) + 0.

Теперь упростим его:

(0 × 1 × 0) + (1 × 1 × 1) + 0 = 0 + 1 + 0 = 1.

Результат вычисления, равный 1, означает «да», «истина», котенок нашел свой дом. (Кроме того, он оказался самым милым!)

Позже в тот же вечер, пока котенок спит у вас на коленях, вы спрашиваете себя, нельзя ли подключить несколько переключателей к лампочке для облегчения процесса проверки котят на соответствие вашим критериям. (Да, вы весьма странный ребенок.) Сами не зная того, вы вплотную приблизились к решающему концептуальному прорыву. Вы вот-вот проведете некоторые эксперименты, которые объединят алгебру Джорджа Буля с электричеством и сделают возможным проектирование и сборку компьютеров, работающих с двоичными числами. Однако пусть вас это не пугает.