Чарльз Петцольд - Код. Тайный язык информатики

Чтобы поставить такой эксперимент, вы, как обычно, соединяете лампочку и батарейку, но используете два переключателя вместо одного.

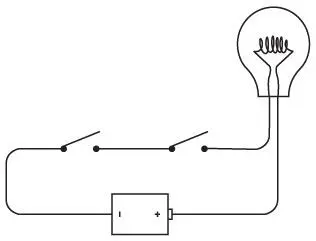
Считается, что переключатели, подключенные друг за другом, соединены последовательно . Если вы замыкаете левый переключатель, ничего не происходит.

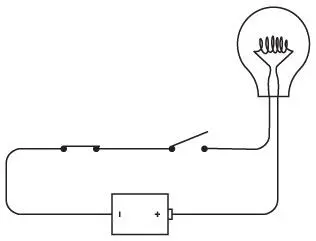
Если вы оставляете левый переключатель разомкнутым, а замыкаете правый, также ничего не произойдет. Лампочка загорается, когда и левый, и правый переключатели оказываются замкнутыми.

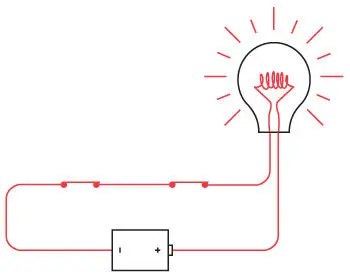
Ключевым в данном случае является союз «и». Левый и правый переключатели должны быть замкнуты, чтобы ток шел по цепи.

Эта схема решает небольшую логическую задачу. Фактически лампочка отвечает на вопрос: «Замкнуты ли оба переключателя?» Мы можем суммировать результаты работы этой схемы в следующей таблице.

Левый переключатель

Правый переключатель

Лампочка

Разомкнут

Разомкнут

Не горит

Разомкнут

Замкнут

Не горит

Замкнут

Разомкнут

Не горит

Замкнут

Замкнут

Горит

В предыдущей главе мы говорили о том, как с помощью двоичных цифр, или битов, можно представить любую информацию, начиная от чисел и заканчивая направлением большого пальца Роджера Эберта. Мы могли сказать, что ноль бит означает, что палец направлен вниз, а один бит — что палец направлен вверх. Переключатель может находиться в двух положениях, поэтому для его описания достаточно одного бита. Можно сказать, что 0 — это «переключатель разомкнут», а 1 — «переключатель замкнут». Лампочка также имеет два состояния, следовательно, для их описания достаточно одного бита. Можно сказать, что 0 — «лампочка не горит», а 1 — «лампочка горит». Теперь мы просто переписываем приведенную выше таблицу.

Левый переключатель

Правый переключатель

Лампочка

0

0

0

0

1

0

1

0

0

1

1

1

Обратите внимание: если мы поменяем местами левый и правый переключатели, результаты останутся прежними. Нам не обязательно различать переключатели. Именно поэтому таблицу можно переписать так, чтобы она напоминала приведенные И/ИЛИ.

Последовательное соединение переключателей

0

1

0

0

0

1

0

1

Действительно, это соответствует таблице с результатами выполнения булевой операции И.

Эта простая схема фактически выполняет операцию И в булевой алгебре.

Теперь попробуйте соединить два переключателя иначе.

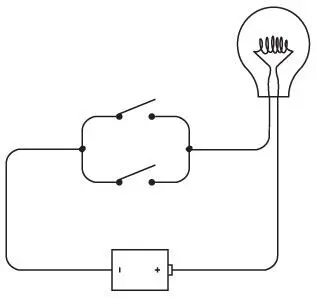
Переключатели соединены параллельно . Разница между этим и предыдущим способом соединения заключается в том, что эта лампочка загорится, если вы замкнете верхний переключатель.

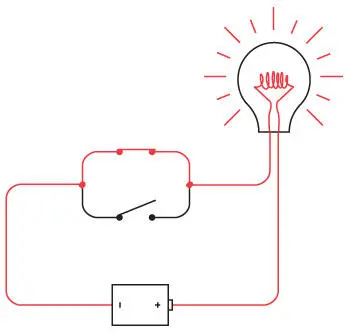
Или нижний переключатель.

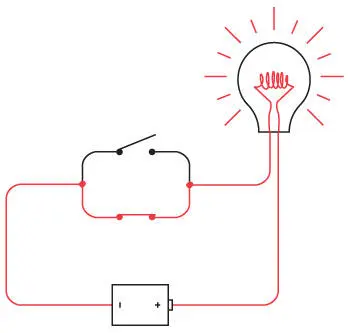
Можно также замкнуть оба переключателя.

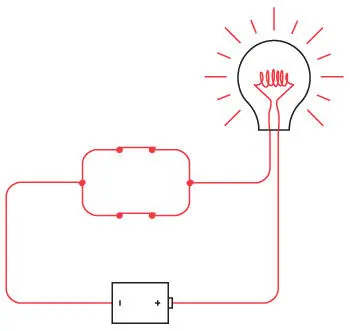
Лампочка загорается, если замкнуть верхний или нижний переключатель. Ключевым словом в данном случае является союз «или».

Опять же, данная схема решает логическую задачу. Лампочка отвечает на вопрос: «Замкнут ли хотя бы один переключатель?» В следующей таблице показаны результаты работы этой схемы.

Левый переключатель

Правый переключатель

Лампочка

Разомкнут

Разомкнут

Не горит

Разомкнут

Замкнут

Горит

Замкнут

Разомкнут

Горит

Замкнут

Замкнут

Горит

Теперь снова используем 0 для обозначения разомкнутого переключателя или негорящей лампочки и 1 — для обозначения замкнутого переключателя или горящей лампочки, в результате чего получим следующую таблицу.

Левый переключатель

Правый переключатель

Лампочка

0

0

0

0

1

1

1

0

1

1

1

1

Опять же ничего не изменится, если переключатели поменять местами, поэтому таблицу можно заполнить следующим образом.

Параллельное соединение переключателей

0

1

0

0

1

1

1

1

Вероятно, вы уже догадались, что эта таблица соответствует результатам булевой операции ИЛИ.

Значит, два соединенных параллельно переключателя выполняют операцию, эквивалентную булевой операции ИЛИ.

Явившись в зоомагазин, вы сказали продавцу: «Мне нужен стерилизованный кот белого или рыжего окраса; или стерилизованная кошка любого окраса, кроме белого; или я возьму любую из имеющихся у вас черных кошек», — и продавец составил такое выражение:

(М × С × (Б + Р)) + (Ж × С × (1 − Б)) + Ч.

Теперь, когда вы знаете, что два соединенных последовательно переключателя выполняют логическую операцию И (обозначаемую символом «×»), а два переключателя, соединенных параллельно, — логическую операцию ИЛИ (обозначаемую символом «+»), вы можете соединить восемь переключателей.

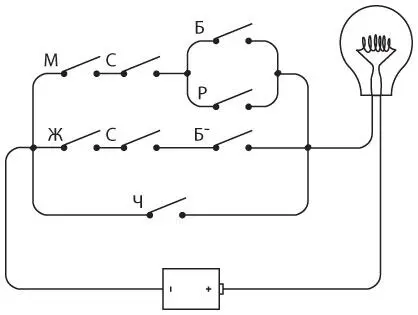
Все переключатели в этой схеме обозначены буквами, соответствующими буквам в булевом выражении. (Б¯ означает НЕ Б и является альтернативным способом записи выражения 1 − Б). Действительно, если вы просмотрите электрическую схему слева направо и сверху вниз, то столкнетесь с буквами в том же порядке, в каком они представлены в выражении. Каждый символ «×» соответствует месту схемы, где два переключателя (или две группы переключателей) соединены последовательно, каждый символ «+» — месту схемы, в котором два переключателя (или две группы переключателей) соединены параллельно.

Как вы помните, продавец сначала принес нестерилизованного рыжего кота. Замкните соответствующие переключатели.

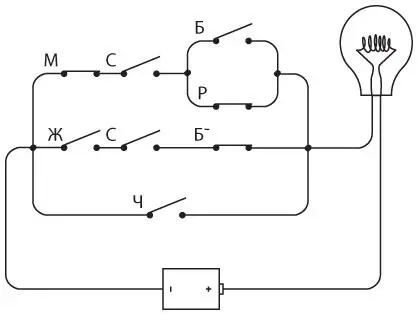
Несмотря на то что переключатели М, Р и НЕ Б замкнуты, лампочка не загорается. Затем продавец принес стерилизованную белую кошку.