Чарльз Петцольд - Код. Тайный язык информатики

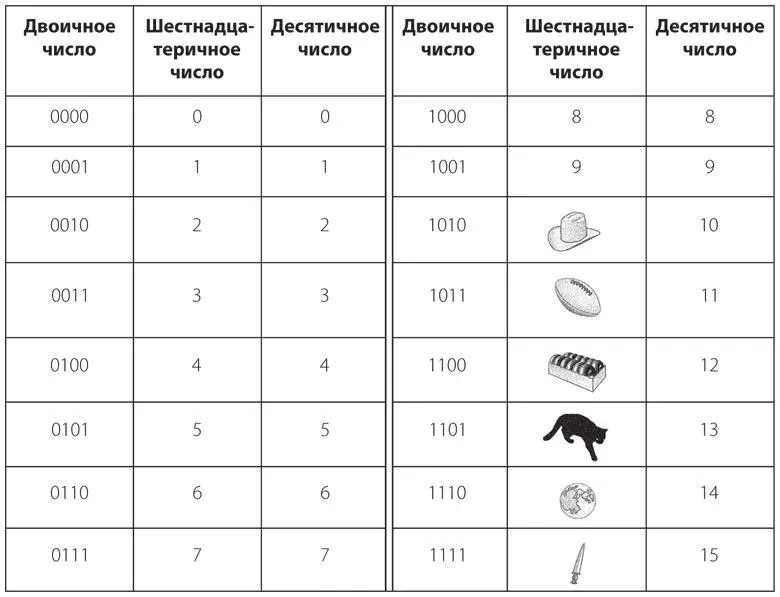
В отличие от символов, используемых для обозначения большинства чисел, у этих обозначений есть преимущество: они легко запоминаются и отождествляются с теми величинами, которые представляют. Существует так называемая десятигаллонная ковбойская шляпа, мяч для американского футбола (11 игроков в команде), дюжина пончиков (12 штук), черная кошка (с которой ассоциируется несчастливое число 13), полная луна (появляется на небе через 14 дней после новолуния) и кинжал (напоминающий об убийстве Юлия Цезаря в 15-й день марта). Каждый байт можно выразить в виде двух шестнадцатеричных цифр. Другими словами, шестнадцатеричная цифра эквивалентна четырем битам, или одной тетраде. В следующей таблице показаны соответствия двоичных, шестнадцатеричных и десятичных чисел.

Вот как можно представить двоичное число 10110110 в шестнадцатеричной системе.

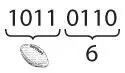
И не важно, имеем ли мы дело с многобайтными числами.

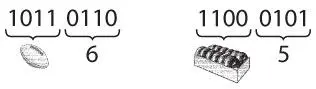
Один байт всегда представляется парой шестнадцатеричных цифр.

К сожалению (а может быть, к счастью), мы не собираемся использовать футбольные мячи и пончики для записи шестнадцатеричных чисел, хотя они, безусловно, могли бы сгодиться для этой цели. Вместо них в шестнадцатеричной системе применяются обозначения, приводящие многих в замешательство. Дело в том, что шесть недостающих шестнадцатеричных цифр представляют шестью первыми буквами латинского алфавита:

0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 …

В следующей таблице показано реальное соответствие между двоичными, шестнадцатеричными и десятичными числами.

Двоичное число

Шестнадцатеричное число

Десятичное число

0000

0

0

0001

1

1

0010

2

2

0011

3

3

0100

4

4

0101

5

5

0110

6

6

0111

7

7

1000

8

8

1001

9

9

1010

A

10

1011

B

11

1100

C

12

1101

D

13

1110

E

14

1111

F

15

Таким образом, двоичное число 10110110 можно представить шестнадцатеричным числом B6, не рисуя футбольный мяч. Как вы помните, в предыдущих главах я указывал основание системы счисления с помощью нижнего индекса, например: 10110110ДВА — для двоичной системы; 2312ЧЕТЫРЕ — для четвертичной; 266ВОСЕМЬ — для восьмеричной; 182ДЕСЯТЬ — для десятичной.

По аналогии мы можем использовать обозначение B6ШЕСТНАДЦАТЬ для шестнадцатеричной системы.

Однако такое выражение чересчур громоздко. К счастью, для шестнадцатеричных чисел существуют и другие, более краткие, обозначения. Вы можете записать такое число следующим образом:

B6HEX.

В этой книге я буду использовать распространенный способ представления шестнадцатеричных чисел, предполагающий добавление к числу строчной латинской буквы h :

B6h.

В шестнадцатеричном числе положение каждой цифры соответствует степени числа 16.

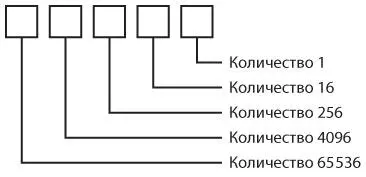
Шестнадцатеричное число 9A48Ch можно представить так:

9A48Ch = 9 × 10000h +

A × 1000h +

4 × 100h +

8 × 10h +

C × 1h.

Это выражение можно записать, используя степени числа 16:

9A48Ch = 9 × 164 +

A × 163 +

4 × 162 +

8 × 161 +

C × 160.

Или десятичные эквиваленты этих степеней:

9A48Ch = 9 × 65 536 +

A × 4096 +

4 × 256 +

8 × 16 +

C × 1.

Обратите внимание на отсутствие двусмысленности при записи отдельных цифр числа (9, А, 4, 8 и C) без нижнего индекса, обозначающего основание системы счисления. Девять — это 9, будь то десятичная или шестнадцатеричная система счисления. С другой стороны, А очевидно представляет шестнадцатеричный эквивалент десятичного числа 10.

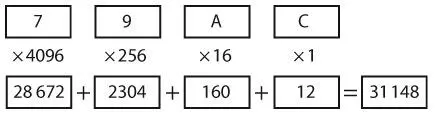
По сути, преобразование всех цифр в десятичные числа позволяет выполнить расчет итогового значения:

9A48Ch = 9 × 65 536 +

10 × 4096 +

4 × 256 +

8 × 16 +

12 × 1.

В итоге получается число 631 948. Таким образом шестнадцатеричные числа преобразуются в десятичные.

Шаблон для преобразования любого четырехзначного шестнадцатеричного числа в десятичное выглядит следующим образом.

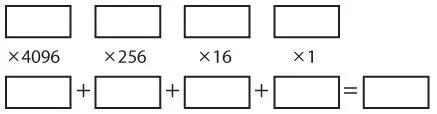
В качестве примера преобразуем число 79ACh. Имейте в виду, что шестнадцатеричные цифры A и C эквивалентны десятичным числам 10 и 12.

Преобразование десятичных чисел в шестнадцатеричные обычно предполагает выполнение операций деления. Число меньшее или равное 255 можно представить одним байтом, состоящим из двух шестнадцатеричных цифр. Чтобы вычислить эти две цифры, нужно разделить число на 16, в результате чего получится частное и остаток. Вернемся к примеру с десятичным числом 182. Разделив 182 на 16, получим 11 (что соответствует цифре B в шестнадцатеричной системе) и 6 в остатке. Так, шестнадцатеричным эквивалентом десятичного числа 182 является B6h. Если десятичное число, которое вы хотите преобразовать, меньше 65 536, то шестнадцатеричный эквивалент будет состоять не более чем из четырех цифр. Шаблон для преобразования такого числа в шестнадцатеричное следующий.

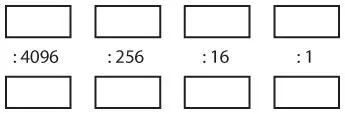
Сначала поместите десятичное число в верхний левый прямоугольник. Это наше первое делимое. Разделим число на 4096 (первый делитель). Частное впишем в прямоугольник, расположенный под делимым, а остаток — в прямоугольник справа от делимого. Этот остаток — новое делимое, которое мы разделим на 256. Вот как число 31 148 преобразуется в шестнадцатеричный формат.

Десятичные числа 10 и 12 соответствуют шестнадцатеричным цифрам A и C, поэтому результат равен 79ACh.

Одна из проблем этой техники заключается в том, что для деления вы, вероятно, решите использовать калькулятор, а калькуляторы не показывают остаток от деления. Если вы разделите 31 148 на 4096 на калькуляторе, то получите 7,6044921875. Чтобы рассчитать остаток, нужно умножить 4096 на 7 (получится 28 672) и вычесть это значение из 31 148. Или умножить 4096 на 0,6044921875 — дробную часть результата от деления. (Правда, некоторые калькуляторы предусматривают функцию преобразования десятичных чисел в шестнадцатеричные и обратно.)