Алексей Данилов - Популярная аэрономия

Мы уже знаем о "важном параметре с длинным названием" - эффективном коэффициенте рекомбинации α'. До сих пор он интересовал нас только выше 100 км, в областях Е и F. Настало время поговорить об этом параметре в сложных условиях D-области. В том, что условия сложные, убеждает все сказанное ранее в данной главе. Насколько при этом все непросто и с эффективным коэффициентом рекомбинации, должен показать этот параграф.

Прежде всего, сложности начинаются с обозначений. Выше 100 км эффективный коэффициент рекомбинации обозначают α' или в худшем случае (если есть проблемы с печатанием штриха) αэф. И никому не придет в голову называть его, скажем, φ или k.

А вот в области D существуют два обозначения: α' (или, что то же, αэф) и ψ. Но дело, конечно, не в самом факте существования двух букв - символов для одного параметра (это-то пережить можно!), а в том, что разные авторы вкладывают разный смысл в само понятие "эффективный коэффициент рекомбинации" и связывают различие в смысле с различием в обозначениях. Чтобы объяснить это подробнее, вернемся на время к простенькой математике уравнения непрерывности.

Уравнение непрерывности для электронов в случае отсутствия отрицательных ионов и при пренебрежении динамическими процессами имеет вид

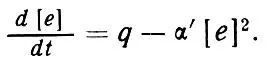Формула 38

Здесь за α' стоит совокупность процессов диссоциативной рекомбинации, приводящих к гибели заряженных частиц.

В области D время жизни заряженных частиц за счет очень быстрых фотохимических процессов мало. А значит, динамика не может угнаться за фотохимией и в уравнении (38) ее можно не учитывать. Но вот отрицательные ионы... Они-то и порождают, как мы знаем, добрую половину проблем D-области. Как они повлияют на вид уравнения (38)? Ведь теперь существуют уже два процесса гибели заряженных частиц: известная нам диссоциативная рекомбинация и взаимная нейтрализация положительных и отрицательных ионов.

Оказывается, уравнение непрерывности теперь выглядит несколько иначе:

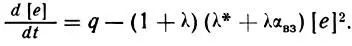Формула 39

Здесь все обозначения нам знакомы, кроме авз - коэффициента скорости той самой реакции взаимной нейтрализации между Х- и Х+. Уравнения (38) и (39) очень похожи по форме. Разница лишь в том, что в последнем случае перед множителем [е]2 стоят два множителя, а не один. И если один из множителей обозначить α', то подобие двух формул будет почти полное. Вот только какой из множителей назвать эффективным коэффициентом рекомбинации и как обозначить? Тут-то и зарыта собака. Одни исследователи, сохраняя единство формы записи уравнения непрерывности для всех ионосферных областей, называют эффективным коэффициентом рекомбинации и обозначают α' все выражение (1+λ) (α*+λαвз), стоящее перед [е]2. В этом случае, естественно, уравнение (39) просто превращается в уравнение (38). Другие же исследователи всю величину (1+λ) (α*+λαвз) обозначают ψ, а под α' понимают только(α*+λαвз), причем разные авторы, использующие эти обозначения, не сходятся в том, какой из параметров (α' или ψ)) следует считать (и называть) эффективным коэффициентом рекомбинации. Представляете, какая получается путаница! Чтобы избежать ее по крайней мере на этих страницах, мы будем следовать первой из описанных точек зрения и считать, что эффективный коэффициент рекомбинации α' равен (1+λ) (α*+λαвз).

Покончив для себя с терминологической путаницей, давайте вернемся к физике. О чем говорят нам уравнения (39) и (38)? О том, что в равновесных условиях (d[e]/dt=0) электронная концентрация на заданной высоте в области D должна быть пропорциональна корню квадратному из g. Если, конечно, эффективный коэффициент рекомбинации на этой высоте не меняется с изменением условий. Долгое время так и считали, поскольку по сути своей α должен являться константой, характеризующей данную высоту. Однако новые данные принесли и новые идеи...

Попробовали сопоставить изменения во времени g и [е] на фиксированных высотах (естественно, для этого надо уметь одновременно измерять оба параметра - задача очень непростая!). И, о ужас, получили совсем другую связь между [е] и g, чем ожидалось. Не g∞[e]2 (как дает (39) при d[e]/dt=0 и α' = const), а g∞[e]. И вывод с большой точностью получился одинаковый, хотя разные авторы, проводившие такие сравнения, использовали разные условия и различные наборы данных о g и [е]. Никуда не денешься, для высот 65-85 км получается линейная связь между скоростью ионизации и электронной концентрацией. Как же это увязать с уравнением (38)? Возможность только одна - предположить, что α' не постоянен, а зависит от условий и изменяется (на заданной высоте) примерно обратно пропорционально электронной концентрации (α'∞1/[е]).

Вывод, на первый взгляд, весьма одиозный. Однако, оглядевшись вокруг, ученые нашли этому выводу ряд подтверждений среди других фактов. Например, во время солнечных вспышек.

Известно, что на солнечные вспышки сильнее всего реагирует именно область D. Испущенное во время вспышки мощное рентгеновское излучение относительно свободно проходит основную часть ионосферы, но, поглощаясь на высотах 70 - 90 км, приводит к резкому увеличению ионизации на этих высотах. Сам эффект был известен давно. Но лишь относительно недавно, когда стали контролировать поток рентгеновского излучения Солнца на искусственных спутниках Земли, удалось сделать количественное сравнение степени возрастания g и [е] (большой вклад в это внесли индийский ученый А. Митра и его сотрудники).

Оказалось, что эффективный коэффициент рекомбинации, вычисленный из

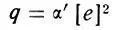Эффективный коэффициент рекомбинации

по наблюденным g и [е], во время вспышки не остается постоянным. Величина α=g/[e]2 падает с развитием эффекта вспышки (см. рисунок) и достигает минимума примерно тогда же, когда наблюдается максимум электронной концентрации. Значит, мы приходим к тому же выводу, что и раньше (но теперь для специфических условий вспышки, где надежность экспериментальных данных выше), - с увеличением [е] падает α'. Значит, изменчивость α' и обратная зависимость его от изменения [е] - факт, видимо, реальный.

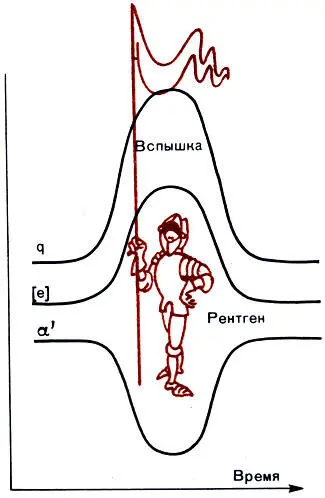Вспышка

Как всегда, обнаружив экспериментальный факт, обратились к теории. Что она может на это сказать? Может ли (и если да, то чем) быть вызвано изменение α' в зависимости от условий? Теория ответила, что этот вопрос должен по-разному решаться на высотах, где есть отрицательные ионы и где их практически нет. Следуя за ней, и. мы рассмотрим вопрос отдельно для верхней и для нижней частей области D, взяв, как мы договорились, в качестве характерных высот 80 и 70 км соответственно.