Макс Тегмарк - Жизнь 3.0. Быть человеком в эпоху искусственного интеллекта

Исследователи из MIT Норман Марголус и Томмазо Тоффоли придумали слово “ computronium ” (компьютрониум), обозначающее любую субстанцию, которая может выполнять любые вычисления. Мы только что убедились, что создать компьютрониум не так уж и сложно: эта субстанция всего лишь должна быть способна соединять гейты NAND друг с другом любым желаемым способом. Разумеется, существуют и мириады других компьютрониумов. Например, еще один легко создать из предыдущего, заменив все гейты NAND на NOR: у него на выходе будет 1 только тогда, когда на оба входа подается 0. В следующем разделе мы обсудим нейронные сети, которые также способны выполнять произвольные вычисления, то есть и они ведут себя как компьютрониум. Ученый и предприниматель Стивен Вольфрам показал, что то же может быть сказано о простых устройствах, получивших название клеточных автоматов, которые периодически подправляют каждый бит в зависимости от того, в каком состоянии находятся биты по соседству. А еще в 1936 году Алан Тьюринг доказал в своей ставшей ключевой статье, что простая вычислительная машина (известная сейчас как “универсальный компьютер Тьюринга”), способная оперировать некоторыми символами на бумажной ленте по некоторым правилам, также способна выполнять любые вычисления. Одним словом, материя не просто обладает способностью к любым вполне определенным вычислениям, но и может производить их самыми разнообразными способами.

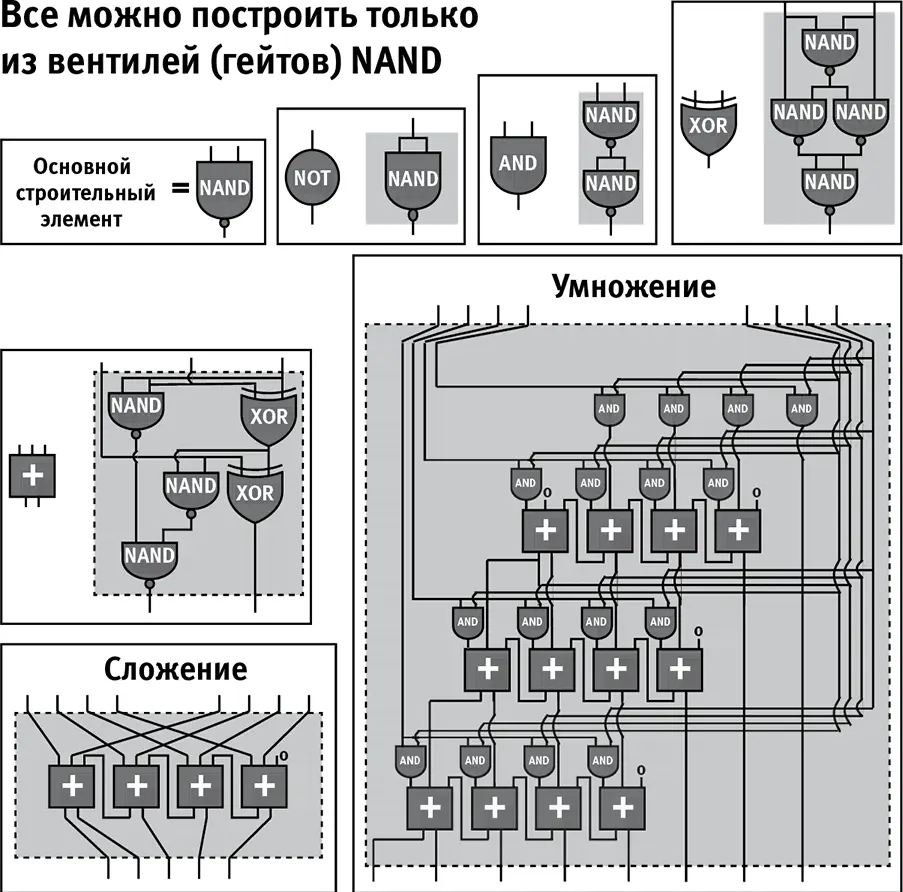
Рис. 2.7

Любое вполне определенное вычисление может быть выполнено при помощи комбинации гейтов одного-единственного типа NAND. Например, у модулей, выполняющих сложение и умножение и представленных на рисунке выше, на вход подается по два бинарных числа, каждое из которых представлено 4 битами, а на выходе получается бинарное число, представленное 5 битами в первом случае, и бинарное число, представленное 8 битами во втором. Менее сложные модули NOT, AND, XOR и “+” (сложение трех одиночных битов в бинарное число, представляемое 2 битами) комбинируются из гейтов NAND. Полное понимание этой схемы исключительно сложно и абсолютно не нужно для дальнейшего чтения книги; я поставил ее здесь исключительно для иллюстрации идеи универсальности, ну и потакая своему внутреннему гику.

Как уже говорилось, Тьюринг в своей памятной статье 1936 года доказал также кое-что значительно более важное: если только компьютер обладает способностью производить некий весьма незначительный минимум операций, он универсален – в том смысле, что при достаточном количестве ресурсов он может сделать все то, на что способен любой другой компьютер. Он доказал универсальность “компьютера Тьюринга”, а приближая его к физическому миру, мы только что показали, что семейство универсальных компьютеров включает в себя такие разные объекты, как сеть гейтов NAND или сеть соприкасающихся нейронов. Более того, Стивен Вольфрам заявил, что большая часть нетривиальных физических систем, от меняющейся погоды до мыслящего мозга, становятся универсальным компьютером, если позволить им как угодно менять свои размеры и не ограничивать их во времени.

Этот самый факт – а именно, что одно и то же вычисление может быть произведено на любом универсальном компьютере, как раз и означает, что вычисление не зависит от субстрата в том же самом отношении, в каком от него не зависит информация: каков бы физический субстрат ни был, оно живет там свою жизнь. Если вы – суперумный персонаж какой-то компьютерной игры будущего, обладающий сознанием, вам никогда не удастся узнать, породила ли вас рабочая станция под Windows, MacBook под MacOS или смартфон с Android, потому что вы субстрат-независимы. У вас не окажется и никаких способов определить, какого рода транзисторы используются микропроцессором этого компьютера.

Поначалу эта базовая идея субстрат-независимости привлекла меня тем, что у нее есть большое количество красивых иллюстраций в физике. Например, волны: у них есть разнообразные свойства – скорость, длина волны, частота, и физики могут решать связывающие их уравнения, совершенно не думая о том, как именно субстрат тут волнуется. Если вы слышите что-то, то вы регистрируете звуковые волны, распространяющиеся в той смеси газов, которую мы называем воздухом, и мы можем рассчитать относительно этих волн все что угодно – что их интенсивность уменьшается как квадрат расстояния, или как они проходят через открытую дверь или отражаются от стен, производя эхо, – ничего не зная о составе воздуха. На самом деле нам даже не обязательно знать, что он состоит из молекул: мы можем отвлечься ото всех подробностей относительно кислорода, азота или углекислого газа, потому что единственная характеристика этого субстрата, которая имеет значение и которая входит в знаменитое волновое уравнение, – это скорость звука, которую нам несложно померить и которая в данном случае будет равна примерно 300 метрам в секунду. Я рассказывал об этом волновом уравнении своим студентам на лекциях прошлой весной и говорил им, в частности, о том, что его открыли и им стали успешно пользоваться еще задолго до того, как физики установили, что молекулы и атомы вообще существуют!

Этот пример с волновым уравнением позволяет сделать три вывода. Во-первых, независимость от субстрата еще не означает, что без субстрата можно обойтись, но только лишь – что многие подробности его устройства не важны. Вы не услышите никакого звука в безвоздушном пространстве, но если замените воздух каким-нибудь другим газом, разницы не заметите. Точно так же вы не сможете производить вычисления без материи, но любая материя сгодится, если только ее можно будет организовать в гейты NAND, в нейронную сеть или в какие-то другие исходные блоки универсального компьютера. Во-вторых, субстрат-независимые явления живут свою жизнь, каков бы субстрат ни был. Волна пробегает по поверхности озера, хотя ни одна из молекул содержащейся в нем воды не делает этого, они только ходят вверх и вниз наподобие футбольных фанатов, устраивающих “волну” на трибуне стадиона. В-третьих, часто нас интересует именно не зависящий от субстрата аспект явления: серфера обычно заботят высота волны и ее положение, а никак не ее молекулярный состав. Мы видели, что это так для информации, и это так для вычислений: если два программиста вместе ловят глюк в написанном ими коде, они вряд ли будут обсуждать транзисторы.

Мы приблизились к возможному ответу на наш исходный вопрос о том, как грубая физическая материя может породить нечто представляющееся настолько эфемерным, абстрактным и бестелесным, как разум: он кажется нам таким бестелесным из-за своей субстрат-независимости, из-за того, что живет своей жизнью, которая не зависит от физических деталей его устройства и не отражает их. Говоря коротко, вычисление – это определенная фигура пространственно-временного упорядочения атомов, и важны здесь не сами атомы, а именно эта фигура! Материя не важна.