Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния

Еще более новаторским, чем использование статистики, было включение философии кибернетики в свой тренерский процесс. Он был первым тренером, который рассматривал футбольную команду как математическую систему. Джонатан Уилсон, автор книги « Переворачивая пирамиду: История футбольной тактики », пишет, что Лобановский видел футбол как «две подсистемы из 11 элементов, движущихся в пределах определенной области и подверженных ряду ограничений». Для Лобановского примечательным свойством футбола было то, что «эффективность подсистемы была выше, чем сумма эффективностей составляющих ее элементов» [83] Цитата из статьи Джонатана Уилсона. Полный текст: www.theguardian.com/football/blog/2011/may/12/valeriy-lobanovskyi-dynamo-kyiv. . Он первым понял, что производительность команды может стать выше суммы производительности ее частей.

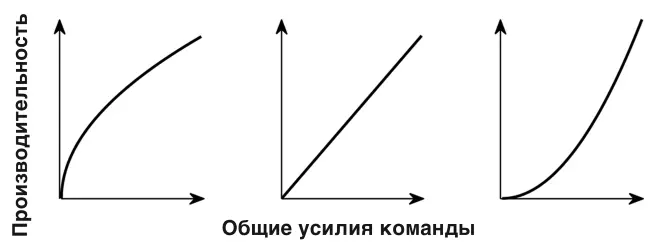
Рисунок 8.1. Три кривые производительности команды: сублинейная (слева), линейная (посередине) и сверхлинейная (справа).

На рисунке 8.1 показаны три возможные кривые того, как производительность команды может увеличиться по отношению к сумме усилий игроков. На кривой посередине с ростом усилий производительность растет линейно – как прямая линия. Здесь производительность команды точно пропорциональна сумме усилий игроков. В левой кривой производительность растет сублинейно и пропорциональна квадратному корню усилий. Теперь производительность меньше суммы усилий игроков. Справа производительность растет сверхлинейно и пропорциональна квадрату усилий: производительность команды теперь больше, чем сумма индивидуальных усилий [84] Три кривые связывают производительность р с усилием х . Линейная кривая p = 10 x , сублинейная кривая равна p = √32 x , суперлинейная – p = x 2 . .

Кривая производительности команды зависит от того, как она играет. Из сублинейной кривой следует, что производительность команды меньше суммы производительности ее частей, то есть имеет некоторую форму избыточности. Представьте себе форварда, который уже накрыт компетентным защитником. Если еще один защитник будет опекать этого нападающего, тому будет немного сложнее забить гол, но повышение эффективности защиты – и команды в целом – будет незначительным. Чем больше защитников опекают игрока, тем меньше отдача.

Лобановский утверждал, что такого типа избыточности следует избегать. Игроки должны доверять друг другу, чтобы выполнять свои индивидуальные роли и находить способ создания нового пространства и движения. Важно, чтобы игроки синхронизировали свои движения. Если один игрок не работает, вся команда разваливается. Футбольная команда может и должна быть суперлинейной. Современные тренеры согласятся с Лобановским. Выбор позиции, сети передач и время рывков зависят от объединения усилий игроков. Эти факторы делают игру команды гораздо более эффективной, чем просто сумма составляющих. Если мы рассчитаем общее усилие команды относительно ее производительности, мы ожидаем, что она будет расти сверхлинейно, как на кривой справа (рисунок 8.1). Если производительность профессиональной команды меньше суммы ее игроков, тут-то и возникают проблемы.

Суперлинейные команды эволюционировали за миллионы лет до рождения Лобановского; чтобы найти эти команды, вам не придется смотреть дальше сада за своим домом. Муравьиные колонии состоят из тысяч взаимозаменяемых частей. Каждый муравей вносит свой вклад в сбор пищи и выращивание новых муравьев; но если один муравей исчезает, есть много других, которые могут взять на себя его роль. Это делает муравьиные колонии идеальной системой для изучения командной работы. Вопрос, на который я и моя коллега, голландский биолог Мадлен Бикман, намереваемся найти ответ, заключается в том, как количество муравьев в колонии влияет на производительность. Увеличится ли она, если колония увеличивается в размерах?

Чтобы ответить на этот вопрос, Мадлен вытащила пылесос для муравьев. Она использовала его для всасывания насекомых из одной колонии и внесения их в другую, что позволило ей создавать муравьиные колонии размером от ста до нескольких тысяч особей. Муравьи взаимодействуют, оставляя дорожку из феромона (химического сигнала), когда они находят еду. Если один муравей оставит феромонный след, а другой муравей найдет его до того, как тот испарится, тогда второй муравей также найдет еду, после чего тоже оставит феромон. Вопрос в том, что произойдет раньше – феромон испарится или другой муравей подкрепит след? Вероятность этих событий зависит как от размера колонии, так и от того, сколько муравьев уже на дорожке. В небольших колониях менее вероятно, что другой муравей успеет найти след, но в больших колониях это гораздо более вероятно.

Обратив это словесное описание в математическую модель, мы смогли предсказать кривую производительности команды для муравьев [85] Beekman, M. Phase transition between disordered and ordered foraging in Pharaoh’s ants. – Proceedings of the National Academy of Sciences 98(17), 2001. – p. 9703–9706. . Мы уже видели три теоретические кривые производительности на рисунке 8.1, показывающие, как производительность может увеличиваться сублинейно, линейно или суперлинейно с увеличением усилий. Для муравьев мы предсказали четвертый тип кривой производительности, показанный на рисунке 8.2. Больше нет плавного роста производительности с ростом усилий: вместо этого есть две отдельные линии для производительности с разрывом между ними. Нижняя линия на рисунке 8.2 представляет собой изолинию производительности, верхняя же отображает результативную производительность. Указывающая вниз стрелка на отметке 300 муравьев показывает, что маленькие колонии будут всегда неуспешны в сборе пищи, стремясь к изолинии. Стрелка вверх на 1100 показывает, что более крупные колонии всегда будут работать лучше. Мадлен подтвердила оба этих предсказания в своих экспериментах. Маленькие колонии не могли сделать феромонную тропу к пище, в то время как большие колонии делали это с легкостью.

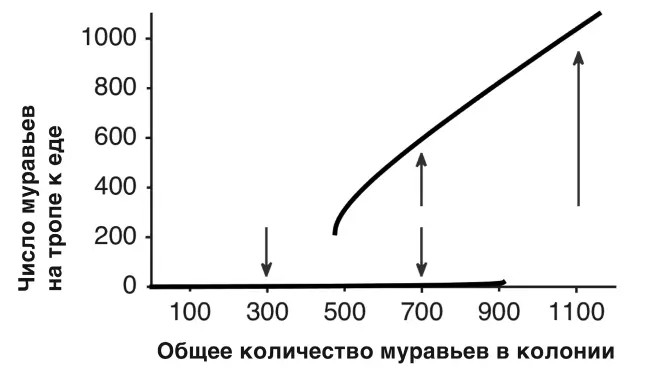
Рисунок 8.2. Кривая производительности группы муравьев. Две сплошные линии показывают, как количество муравьев, нашедших еду, увеличивается с общим количеством муравьев. Нижняя линия – это случай, когда лишь небольшое количество муравьев находят пищу. Верхняя линия – это случай, когда есть достаточно муравьев, чтобы сделать след. Когда много муравьев изначально находят пищу, они достигают верхней линии (обозначена стрелкой вверх); когда находят лишь некоторые, они опускаются до нижней линии (стрелки, указывающие вниз).