Микаэль Лонэ - Большой роман о математике. История мира через призму математики

[ЭД] Галилей Г. Пробирщик / пер. на англ. С. Дрейк: Электрон. ресурс. Режим доступа: http://www.princeton.edu/~hos/h291/assayer.htm

[СГ] Гомес в соавторстве Р. П. Альгамбра. Epsilon, 1987.

[Ч] Гедж Д. Ноль. Pocket, 2008.

Хошкорн Б., Сурро Д. Математика от А до Я. Ellipses, 1996.

[Э] Гильберт Д. О будущих проблемах математики – 23 проблемы. Éditions Jacques Gabay, 1990.

[ЭЛ] Хофштадтер Д. Гёдель, Эшер, Бах: эта бесконечная гирлянда. Dunod, 2000.

[AЧ] Хойруп Й. Алгебра во времена Вавилона. Vuibert – Adapt Snes, 2010.

[AЧ] Хойруп Й. Происхождение – математика, место и время. CNRS Éditions, 2009.

[A] Ямвлих. Жизнь Пифагора. La roue À livres, 2011.

[Ч] Кит М. по Э. По. По мотивам «Ворона»: Электрон. ресурс. Режим доступа: http://cadaeic.net/naraven.htm, 1995.

[СЧ] Келлер А. Математические загадки в Южной Индии. Maths Express au carrefour des cultures, 2014.

[СЧ] аль-Хорезми М. Алгебра / пер. на англ. Ф. Розена. Oriental Translation Fund, 1831.

[А] Лаэртский Д. Жизнь, доктрина и суждения видных философов. GF-Flammarion, 1965.

[ЭТ] Лоней М. Взаимодействующие урны: Дис. … канд. матем. наук. Университет Экс-Марсель, 2012.

[ЭГ] Мандельброт Б. Фрактальные объекты. Champs Science, 2010.

Мель С. ChronoMath, хронология и словарь математики: Электрон ресурс. Режим доступа: http://serge.mehl.free.fr/

[С] Мойон M. Перевести математику на андалусский в XII веке. Maths Express au carrefour des cultures, 2014.

[ЭЛ] Нагель E., Ньюмен Дж. Р., Гедель К. и Жирар Ж.-И. Теорема Гёделя. Points. 1997.

[РЧ] Наполитани П. Д. Итальянский Ренессанс – математика, место и время. CNRS Éditions, 2009.

[ЭД] Ньютон И. Математические начала натуральной философии. Dunod 2011.

Дю Сотой М. Симметрия или математика в лунном свете. Éditions HÉloïse d’Ormesson, 2012.

[ЭТ] Паскаль Б. Трактат об арифметическом треугольнике. Г. Деспре, 1665.

Петерс А. Синхроноптическая история мира. Éditions acadÉmiques de Suisse – Bâle.

[АГ] Платон. Тимей. GF-Flammarion, 1999.

[СЧ] Плофкер K. Индия в эпоху Античности и Средневековья – математика, место и время. CNRS Éditions, 2009.

[Э] Пуанкаре А. Наука и метод. Flammarion, 1908.

[ЭТ] Пойа Д. О некоторых моментах теории вероятности. Архив Института А. Пуанкаре, 1930.

[АЧ] Пруст К. Краткая хронология истории математики в Месопотамии. CultureMATH, 2006. Электрон. ресурс. Режим доступа: http://culturemath.ens.fr/content/brève-chronologie-delhistoire-des-mathÉmatiques-en-mÉsopotamie.

[АЧ] Пруст К. Шестидесятеричная система счисления в Месопотамии. CultureMATH, 2005. Электрон. ресурс. Режим доступа: http://culturemath.ens.fr/content/le-calcul-sexagÉsimal-en-mÉsopotamie.

[АЧ] Пруст К. Математика в Месопотамии, образ математики. Электрон. ресурс. Режим доступа: http://images.math.cnrs.fr/Mathematiques-en-Mesopotamie.html, 2014.

[А] Пифагор. Золотые стихи. Adyar, 2009.

[ЭЛ] Рассел Б., Уайтхед А. Н. Принципы математики. Merchant Books, 2009.

[АЧ] Шмандт-Бессерат Д. От учета к письму // Рафот Б. А., Рубин Д. Л. Социальное конструирование письменной коммуникации. Норвуд: Ablex Publishing Co., 1988.

[АЧ] Шмандт-Бессерат Д. Эволюция письменности: Электрон. ресурс. Режим доступа: https://sites.utexas.edu/dsb/

[РЧ] Серфати М. и др. Секрет и правила, поиск истины. ACL–Les Éditions du Kangourou, 1999.

[ЭЛ] Смаллиан Р. Теорема Гёделя о неполноте. Dunod, 2000.

[ЭЛ] Смаллиан Р. Как называется эта книга? Dunod, 1993.

[Ч] Стендаль. Жизнь Анри Брюлара. Folio classique, 1973.

[ЭЛ] Тьюринг А. Вычислимые числа с приложением к проблеме разрешимости. Архив Лондонского математического общества, 1936.

[РЧ] Виет Ф. Введение в аналитическое искусство / пер. на фр. А. Вассет. 1630.

Условное название региона на Ближнем Востоке, в котором в зимние месяцы наблюдается повышенное количество осадков.

Пер. Йенс Хойруп, « Алгебра во времена Вавилона », издательство Vuibert / SNES Adapt, 2010.

Согласно условиям задачи, длина и глубина равны, но в вавилонской системе исчисления глубина измерялась единицами в 12 раз большими, чем длина.

Необходимо отметить, что в шестидесятичной системе исчисления 1’10 обозначает число, равное «одной целой десяти шестидесятых», что в нашей системе исчисления соответствует 7/6. ’50, в свою очередь, обозначает 5/6 (или пятьдесят шестидесятых).

Наклон грани пирамиды, который также назывался по-египетски секед, – это горизонтальное расстояние между двумя точками, высота которых отличается на один локоть.

Перевод Карин Чемла и Шучан Гао « Математика в девяти книгах », изд. Dunod, 2005.

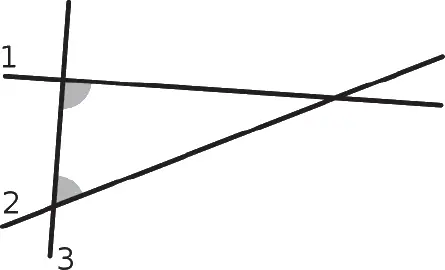
Эта аксиома сложнее, чем четыре первые, что породило многочисленные дебаты между математиками. На фигуре ниже видно, что сумма выделенных углов менее двух прямых углов, что означает, что прямые 1 и 2 пересекаются со стороны этих углов

Стихотворение «Ворон», написанное Эдгаром По в 1845 году, было переписано в 1995 году Майклом Китом под названием « По мотивам “Ворона ”» ( Near Raven ), каждое слово которого соответствовало последовательно цифрам в математической константе.

Угломерный прибор.

Угломерный прибор.

Математик из Голландии Людольф Цейлен рассчитал величину π с точностью до 35 знаков после запятой сто семьдесят лет спустя.

√5 обозначает квадратный корень из числа 5, т. е. положительное число, квадрат которого равен 5. Это число приблизительно равно 2,236.

Вычисление суммы бесконечного ряда чисел делается с помощью понятия предела. Данный метод заключается в том, что вместо того, чтобы складывать бесконечные числа ряда, определяется число, к которому стремится искомая сумма. В примере с Ахиллесом и черепахой если сложить первые числа ряда, получится следующий результат: 100 + 50 + 25 + 12,5 + 6,25 + 3,125 + 1,5625 = 198,4375. Если продолжить этот ряд до двадцатого числа, получится приблизительно 199,9998. Можно продемонстрировать, что, добавляя все больше и больше новых чисел ряда, сумма будет бесконечно приближаться к 200. Поэтому считается, что сумма будет равна 200.

Обратите внимание, что значение угла должно быть выражено не в градусах, а в радианах. Так, применительно к данной формуле, полный круг составляет не 360°, а 2π радиан. Это может показаться непривычным, но вычисление суммы данного ряда чисел приведет к правильному результату только при выражении угла в таком виде.

Термин «алгебра» имеет два значения и может обозначать дисциплину либо алгебраическую структуру, именуемую также «алгебра над полем».

Октаэдр – одно из пяти Платоновых тел, с которым мы уже ранее сталкивались. Усеченный октаэдр получается путем отсечения вершин октаэдра таким же образом, как получался усеченный икосаэдр (форма футбольного мяча) путем отсечения вершин икосаэдра.