Коллектив авторов - На плечах гигантов

Пусть имеется координатная система, в которой справедливы уравнения механики Ньютона. С целью отличить эту координатную систему от вводимых позже координатных систем и для уточнения терминологии назовем ее «покоящейся системой».

Если относительно покоящейся системы некоторая материальная точка находится в покое, то положение этой точки относительно такой координатной системы может быть определено методами евклидовой геометрии с помощью твердых масштабов и выражено в декартовых координатах.

Если мы хотим дать описание движения какой-нибудь материальной точки, то мы задаем значения ее координат как функций времени. При этом нужно иметь в виду, что такое математическое описание имеет физический смысл только тогда, когда предварительно установлено, что подразумевается под «временем». Другими словами, необходимо обратить внимание на то, что все наши выводы, в которых как-то задействовано время, всегда являются выводами об одновременных событиях. Если я, например, говорю: «Этот поезд прибывает сюда в 7 часов», – то это означает примерно следующее: «Указание маленькой стрелки моих часов на 7 часов и прибытие поезда суть одновременные события» [8].

Возможно, время нельзя уподобить одной-единственной железнодорожной ветке, которая ведет из точки А в точку В: оно, как и настоящая железная дорога, способно закладывать петли или радикально менять направление.

На первый взгляд может показаться, что все трудности определения «времени» могут быть преодолены, если вместо слова «время» написать «положение маленькой стрелки моих часов». Такое определение, действительно, достаточно в том случае, когда речь идет об определении времени только для того самого места, в котором как раз находятся часы. Однако такого определения уже недостаточно, как только речь пойдет о связи друг с другом во времени ряда событий, протекающих в различных местах. Или, что то же самое, когда речь пойдет об установлении времени для тех событий, которые происходят в местах, удаленных от часов.

Для того чтобы определить время событий, мы могли бы, конечно, удовлетвориться тем, что заставили бы некоторого наблюдателя, находящегося с часами в начале координат, сопоставлять соответствующее положение стрелки часов с каждым световым сигналом, идущим к нему через пустоту и дающим знать о регистрируемом событии. Однако такое сопоставление связано с тем неудобством, известным нам из опыта, что оно не будет независимым от местонахождения наблюдателя, снабженного часами. Мы придем к гораздо более практическому определению путем следующих рассуждений.

Поместим часы в точке А пространства. Тогда наблюдатель, находящийся в А , может устанавливать время событий в малой окрестности А, наблюдая одновременные с этими событиями положения стрелок часов. Если в другой точке В пространства также имеются часы (мы добавим: точно такие же часы, как в точке А ), то в малой окрестности В также возможна временная оценка событий находящимся в В наблюдателем. Однако невозможно без дальнейших предположений сравнивать во времени какое-либо событие в А с событием в В, потому что мы определили пока только « А -время» и « В -время», но не общее для А и В «время». Последнее можно установить, вводя определение, что «время», необходимое для прохождения света из А в В , равно «времени», требуемому для прохождения света из В в А . Пусть в момент t A по « А -времени» луч света выходит из А в В , отражается в момент t B по « B -времени» от В к А и возвращается назад в А в момент t’ A по « А -времени». Часы в А и В будут идти, согласно определению, синхронно, если

Допустим, что данное определение синхронности можно дать однозначным образом и, кроме того, для сколь угодно большого числа точек и что, таким образом, справедливы следующие утверждения:

1) если часы в В идут синхронно с часами в А , то часы в А идут синхронно с часами в В ;

2) если часы в А идут синхронно как с часами в В , так и с часами в С , то часы в В и С также идут синхронно относительно друг друга.

Таким образом, пользуясь некоторыми (мысленными) физическими экспериментами, мы установили, что нужно понимать под синхронно идущими, находящимися в различных местах покоящимися часами, и благодаря этому, очевидно, достигли определения понятий: «одновременность» и «время». «Время» события – это одновременное с событием показание покоящихся часов, которые находятся в месте события и которые идут синхронно с некоторыми определенными покоящимися часами, причем с одними и теми же часами при всех определениях времени.

Согласно опыту, будем также считать, что величина есть универсальная постоянная (скорость света в пустоте).

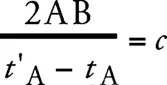
Существенным является то, что мы определили время с помощью покоящихся часов в покоящейся системе. Такое время, принадлежащее к покоящейся системе, будем называть «временем покоящейся системы».

Последующие соображения опираются на принцип относительности и на принцип постоянства скорости света. Мы формулируем оба принципа следующим образом.

1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.

2. Каждый луч света движется в «покоящейся» системе координат с определенной скоростью V , независимо от того, испускается ли этот луч света покоящимся или движущимся телом.

При этом

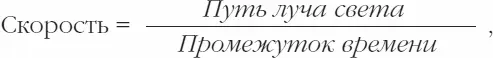
причем «промежуток времени» следует понимать в смысле определения в § 1.

Рассмотрим покоящийся твердый стержень, и пусть его длина, измеренная также покоящимся масштабом, есть l . Пусть теперь стержню, ось которого направлена по оси X покоящейся координатной системы, сообщается равномерное и параллельное оси X поступательное движение (со скоростью v ) в сторону возрастающих значений х . Поставим теперь вопрос о длине движущегося стержня, которую мы полагаем определенной с помощью следующих двух операций: