Коллектив авторов - На плечах гигантов

Невозможно искривить пространство, не затронув время. Значит, у времени есть форма. Тем не менее время, похоже, идет лишь в одном направлении.

До тех пор пока мы ограничиваемся чисто механическими явлениями, для которых справедлива механика Ньютона, мы уверены в равноценности систем К и К’ . Однако представление наше будет достаточно глубоким только в том случае, если системы К и К’ окажутся равноценными относительно всех физических явлений, т. е. если законы природы по отношению к системе К полностью совпадут с законами природы по отношению к системе К’ . Приняв это, мы получаем принцип, имеющий большое эвристическое значение, если он действительно справедлив. Действительно, с помощью теоретического изучения явлений, протекающих относительно равномерно ускоренной координатной системы, можно получить представление о ходе явлений в однородном гравитационном поле. Далее будет прежде всего показано, каким образом с точки зрения обычной теории относительности наша гипотеза приобретает значительную долю вероятности.

Теория относительности привела к выводу о росте инертной массы тела с увеличением содержащейся в нем энергии. Так, если приращение энергии есть Е , то приращение инертной массы составляет Е/с 2 , где с – скорость света. Однако возникает вопрос: соответствует ли такому приращению инертной массы также приращение тяготеющей массы? Если нет, то тогда тело в одном и том же поле тяжести падало бы с разным ускорением, зависящим от энергии самого тела. Такой удовлетворительный результат теории относительности, согласно которому закон сохранения массы содержится в законе сохранения энергии, оказался бы несправедливым, хотя в этом случае для инертной массы и нужно было бы отбросить закон сохранения массы в его старой формулировке, но для тяготеющей массы он остался бы в силе.

Такой вывод очень маловероятен. С другой стороны, обычная теория относительности не дает ни одного аргумента, из которого можно было бы заключить, что вес тела зависит от содержащейся в нем энергии. Однако мы покажем, что из нашей гипотезы об эквивалентности систем отсчета К и К’ с необходимостью вытекает тяжесть энергии.

Итак, пусть две физические системы тел S 1 и S 2 , снабженные измерительными приборами, расположены на оси Z системы отсчета К на расстоянии h друг от друга [12]таким образом, что гравитационный потенциал в том месте, где находится система S 2 , на γh больше гравитационного потенциала в месте нахождения S 1 . Далее, пусть из S 2 посылается в S 1 определенное количество энергии Е в виде излучения и пусть при этом количество энергии измеряется с помощью приборов, которые, будучи установлены в одном и том же месте систем z и там друг с другом сравнены, оказались бы совершенно одинаковыми.

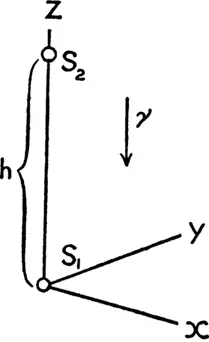
Заметим, что изначально о процессе переноса энергии излучением ничего сказать нельзя, потому что мы не знаем, как влияет поле тяжести на энергию излучения и на измерительные инструменты в S 1 и S 2 . Тем не менее, согласно допущению об эквивалентности систем отсчета К и К’ , мы можем на место системы К , находящейся в однородном поле тяжести, поставить свободную от тяготения систему отсчета К’ , которая движется равномерно ускоренно в направлении положительных значений z , с осью z которой жестко связаны физические системы S 1 и S 2 .

Обсудим процесс переноса энергии излучением из S 2 в S 1 , если мы находимся в некоторой системе отсчета К 0 , не обладающей ускорением. Будем считать, что в тот момент, когда энергия излучения Е 2 переносится из S 2 в S 1 , система К’ обладает относительно системы К 0 нулевой скоростью. Лучи достигнут системы S 1 спустя время h/с (в первом приближении). В этот момент система S 1 обладает относительно К 0 скоростью h/с = v . Таким образом, согласно обычной теории относительности, достигающее S 1 излучение имеет не энергию Е 2 , а большую энергию Е 1 которая в первом приближении связана с Е 2 соотношением [13]:

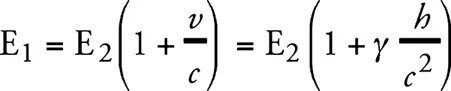
(1)

Согласно сделанному нами предположению, точно такое же соотношение справедливо и в том случае, когда рассматриваемый процесс протекает в системе К – неускоренной, но находящейся в гравитационном поле. В этом случае мы можем заменить γ h потенциалом Ф гравитационного поля в точке, где находится S 2 , если произвольная постоянная потенциала Ф в точке, где находится S 1 , приравнивается нулю. Таким образом, получаем:

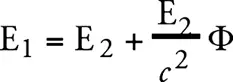
(1а)

Последнее есть закон сохранения энергии для рассматриваемого процесса. Энергия Е 1 , приходящая в S 1 больше, чем измеренная такими же приборами энергия Е 2 , которую отдает система в S 2 , на величину потенциальной энергии массы Е 2 / с 2 в поле тяжести. Таким образом, для выполнения закона сохранения энергии нужно к энергии Е перед ее испусканием из S 2 прибавить потенциальную энергию, которая соответствует (тяжелой) массе Е / с 2 в поле тяжести. Следовательно, наше допущение об эквивалентности систем отсчета К и К’ устраняет изложенную в начале этого параграфа трудность, чего не могла сделать обычная теория относительности.

Смысл полученного результата становится особенно ясным при рассмотрении следующего кругового процесса.

1. Энергия Е , измеренная в S 2 , посылается в форме излучения из S 2 в S 1 , где, согласно только что полученному результату, поглощается энергия Е × (1 + γ h/с 2 ), измеренная в S 1 .

2. Тело W с массой М падает из S 2 в S 1 , и при этом совершается работа M γ h .

3. Энергия Е из системы S 1 переносится на тело W , когда оно находится в S 1 . Благодаря этому изменяется тяжелая масса М, и пусть ее новое значение равно М’ .

4. Тело W снова поднимается в S 2 , и при этом затрачивается работа М’ γ h.