Коллектив авторов - На плечах гигантов

Таким образом, нельзя сказать, что оба часовых механизма, в S 2 и S 1 , показывают правильное «время». Так, если мы определяем время в S 1 часами U , то мы должны измерять время в S 2 часами, которые идут в [1 + (Ф/ с 2 )] раза медленнее, чем часы U, если их сравнить с часами U в одном и том же месте . Это связано с тем, что измеренная подобными часами частота рассмотренного выше луча света при его отправлении из S 2

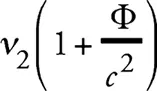
в согласии с формулой (2а), равна частоте v 1 того же луча света при его прибытии в S 1 .

Отсюда вытекает следствие, представляющее фундаментальное значение для теории. Если скорость света измерять в различных местах ускоренной системы отсчета К’ в отсутствие гравитационного поля, пользуясь одинаково идущими часами U , то всюду будет получаться одно и то же значение. Исходя из нашего основного допущения, то же самое справедливо и для системы К . Однако из этого следует, что в местах с разными гравитационными потенциалами при измерении времени необходимо пользоваться по-разному идущими часами. В том месте, которое обладает гравитационным потенциалом Ф относительно начала координат, нужно при измерении времени применять часы, которые при перенесении их в начало координат шли бы в (1 + + Ф/ с 2 ) раза медленнее, чем те часы, которыми определяется время в начале координат. Если мы обозначим через с 0 скорость света в начале координат, то скорость света с в некотором месте с гравитационным потенциалом Ф будет равна

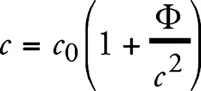
(3)

Согласно этой теории, принцип постоянства скорости света справедлив не в той формулировке, в какой он кладется в основу обычной теории относительности.

Космический корабль пролетает мимо астронавта справа налево со скоростью 4/5 скорости света. Член экипажа испускает импульс света, который попадает в отражатель и возвращается обратно.

Этот свет видят и астронавт-наблюдатель, и пассажиры корабля. Однако они по-разному оценят, какое расстояние прошел свет после отражения.

По Эйнштейну, скорость света одинакова для всех свободно движущихся наблюдателей, хотя у каждого из них будет ощущение своей, отличной от других, скорости света.

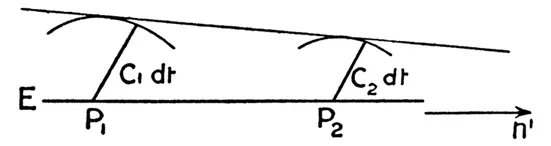
Из только что доказанного положения – скорость света в поле тяжести является функцией места – нетрудно с помощью принципа Гюйгенса доказать, что лучи света, распространяющиеся поперек поля тяжести, должны искривляться. В самом деле, пусть E – плоскость равной фазы некоторой плоской световой волны в момент времени t , а Р 1 и Р 2 – две точки на ней, расстояние между которыми равно единице. Точки Р 1 и Р 2 лежат в плоскости чертежа, которая выбрана так, что взятая по нормали к ней производная от Ф, а следовательно, и от с , обращается в нуль. Описывая около точек Р 1 и Р 2 окружности радиусами c 1 dt и c 2 dt и проводя к ним общую касательную, получаем плоскость равной фазы, точнее, ее сечение плоскостью чертежа для момента времени t + + dt , причем с 1 и с 2 представляют собой скорости света соответственно в точках Р 1 и Р 2 . Следовательно, угол отклонения луча света на пути cdt составляет

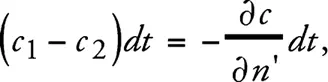
если мы его считаем положительным, когда луч света изгибается в сторону возрастания n’ . Таким образом, угол отклонения на единицу пути луча света будет равен

Наконец, для отклонения α , которое луч света испытывает на любом пути s в сторону n’ , получаем выражение

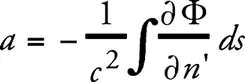
(4)

Такой же результат можно было бы получить также путем непосредственного рассмотрения распространения луча света в равномерно ускоренной системе отсчета К’ , преобразования результата к системе К и затем обобщения на случай гравитационного поля произвольного вида.

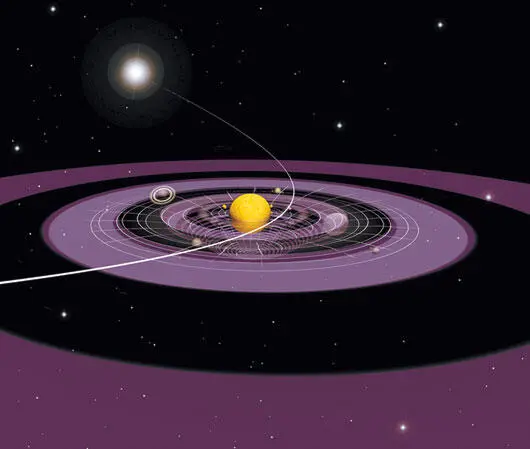
Гравитационное поле массивного тела, например, Солнца, искривляет траекторию света далекой звезды.

Согласно выражению (4), проходящий мимо какого-либо небесного тела луч света испытывает отклонение в сторону убывания гравитационного потенциала, т. е. в сторону небесного тела. Это отклонение есть

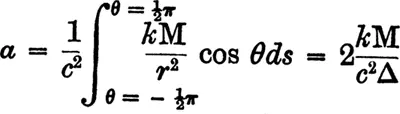
где k – гравитационная постоянная, М – масса небесного тела, Δ – расстояние от луча до центра небесного тела.

Стандартная модель жизни и смерти нашей Вселенной. Без теоретических работ Эйнштейна эта модель не была бы возможна с математической точки зрения.

На этой иллюстрации слева направо – триллионные доли секунды после Большого взрыва, когда Вселенная инфляционно расширяется от размеров меньше атома с массой пакетика сахара до диаметра галактики.

Вселенная продолжает расширяться, и галактики, а с ними и звезды, атомы и частицы расходятся друг от друга все дальше и дальше, и так будет до тех пор, пока Вселенная не станет очень разреженной, пустой и голой. Вторая модель предполагает, что в конце концов ускорение прекратится и Вселенная под воздействием гравитационных сил схлопнется в огромную черную дыру – произойдет Большое сжатие.

По этой причине луч света, проходящий мимо Солнца, испытал бы отклонение, равное 4 × 10 -6= 0,83 секунды дуги . Благодаря искривлению луча угловое расстояние звезды от центра диска Солнца окажется увеличенным на эту величину. Так как звезды в соседних с Солнцем областях неба становятся видимыми при полных солнечных затмениях, то это следствие теории можно сравнить с опытом. Так, для планеты Юпитер ожидаемое смещение достигает примерно 0,01 доли указанного значения. Было бы крайне желательным, чтобы астрономы заинтересовались поставленным здесь вопросом даже и в том случае, если бы предыдущие рассуждения казались недостаточно обоснованными или фантастическими. Действительно, независимо от всякой теории, возникает вопрос: можно ли вообще современными средствами установить влияние гравитационных полей на распространение света.