Всё о метрологии

Важнейшей метрологической характеристикой средств измерений является погрешность.

Под абсолютной погрешностью меры понимается алгебраическая разность между ее номинальным X н и действительным X д значениями:

Δ = X н– X д (84)

а под абсолютной погрешностью измерительного прибора — разность между его показанием X п и действительным значением X д измеряемой величины:

Δ = X п– X д (85)

Абсолютная погрешность измерительного преобразователя может быть выражена в единицах входной или выходной величины. В единицах входной величины абсолютная погрешность преобразователя определяется как разность между значением входной величины X , найденной по действительному значению выходной величины и номинальной статической характеристике преобразователя, и действительным значением X д входной величины:

Δ = X – X д

Однако в большей степени точность средства измерений характеризует относительная погрешность , т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины:

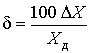. (86)

Обычно δ ≪ 1, поэтому в формулу (86) вместо действительного значения часто может быть подставлено номинальное значение меры или показание измерительного прибора.

Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности , равной отношению абсолютной погрешности измерительного прибора к некоторому нормирующему значению X N :

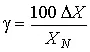. (87)

В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т.д.

Погрешности измерительных средств принято подразделять на статические , имеющие место при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей, и динамические , появляющиеся при измерении переменных величин и обусловленные инерционными свойствами средств измерений.

Согласно общей классификации, статические погрешности измерительных средств делятся на систематические и случайные .

Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности находят при поверке и аттестации образцовых приборов, например, измерением наперед заданных значений измеряемой величины в нескольких точках шкалы. В результате строится кривая или создается таблица погрешностей, которая используется для определения поправок. Поправка в каждой точке шкалы численно равна систематической погрешности и обратна ей по знаку, поэтому при определении действительного значения измеряемой величины поправку следует прибавить к показанию прибора. Так, если поправка к показанию динамометра 120 Н равна +0.6 Н, то действительное значение измеряемой силы составляет 120+0.6=120.6 Н. Удобнее пользоваться поправкой, чем систематической погрешностью, поэтому приборы чаще снабжают кривыми или таблицами поправок.

Систематическую погрешность в функции измеряемой величины можно представить в виде суммы погрешности схемы, определяемой самой структурной схемой средства измерений, и технологических погрешностей, обусловленных погрешностями изготовления его элементов.

Как те, так и другие виды погрешностей можно рассматривать в качестве систематических лишь при измерении постоянной величины с помощью одного экземпляра измерительного прибора. В массе же измерений различных значений физической величины, осуществляемых одним или многими приборами того же типоразмера, эти систематические погрешности приходится относить к классу случайных.

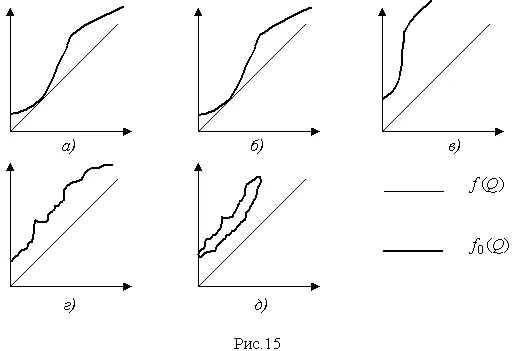
Между погрешностями схемы и технологическими погрешностями средств измерений существует принципиальная разница. Если первые накладывают свой отпечаток на характер изменения по шкале суммарной погрешности всех средств измерений данного типоразмера, то технологические погрешности индивидуальны для каждого экземпляра, т. е. их значения в одних и тех же точках шкалы различны для различных экземпляров приборов. На рис. 15, а показано взаимное положение статических характеристик реального f ( Q ) и идеального f 0( Q ) приборов при наличии только погрешностей схемы. Технологические погрешности в большой степени искажают эту картину.

Результатом их проявления является:

а) поступательное смещение статической характеристики относительно характеристики идеального прибора и возникновение погрешности, постоянной в каждой точке шкалы; эта погрешность называется аддитивной (рис. 15, б );

б) поворот статической характеристики и появление погрешности, линейно возрастающей или убывающей с ростом измеряемой величины и называемой мультипликативной погрешностью (рис. 15, в );

в) нелинейные искажения статической характеристики (рис. 15, г );

г) появление погрешности обратного хода, выражающейся в несовпадении статических характеристик прибора при увеличении и уменьшении измеряемой величины (рис. 15, д ).

Динамические погрешности обусловливаются инерционными свойствами средств измерений и появляются при измерении переменных во времени величин. Типичным случаем является измерение с регистрацией сигнала, изменяющегося со временем. Если x ( t ) и y ( t ) — сигналы на входе и на выходе средства измерений с чувствительностью K , то динамическая погрешность

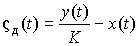. (88)

Для средств измерений, являющихся линейными динамическими системами с постоянными во времени параметрами, наиболее общая характеристика динамических свойств — это дифференциальное уравнение . В этом случае уравнение линейное с постоянными коэффициентами:

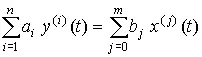, (89)

где y ( i )( t ) и x ( j )( t ) — i -e и j -e производные входного и выходного сигналов; a i и b j — постоянные коэффициенты, n и m – порядок левой и правой частей уравнения, причем n < m . Дифференциальное уравнение является метрологической характеристикой средств измерения, поскольку позволяет при известном сигнале на входе x(t) найти выходной сигнал y(t) и после подстановки их в выражение (83) вычислить динамическую погрешность.