Всё о метрологии

Распределение результата косвенных измерений будет нормальным, если нормальны распределения результатов прямых измерений. В этих условиях для построения доверительного интервала, накрывающего истинное значение измеряемой величины, следует применить нормированную функцию нормального распределения, если число измерений достаточно велико. Если же объемы рядов прямых измерений недостаточно велики, то можно воспользоваться распределением Стьюдента с некоторым “эффективным” числом степеней свободы, которое для рассматриваемого случая при независимости погрешностей измерения ( r XY = 0) подсчитывается по формуле

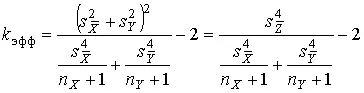, (80)

где n X и n Y — числа прямых наблюдений величин Q X и Q Y .

Если числа наблюдений одинаковы ( n X= n Y= n ), то выражение для эффективного числа степеней свободы распределения Стьюдента упрощается:

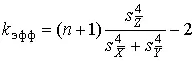. (81)

Итоговый результат измерений записываем в виде:

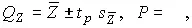
где t p определяется из выражения:

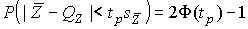
или

.

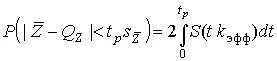Рассмотренные выражения можно использовать и в том случае, когда искомая величина является суммой от измеряемых прямыми способами величин:

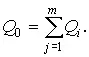(82)

К такой формуле приходим при измерении больших величин по частям, например при измерении длин с помощью концевых мер длины, взвешивании с применением набора гирь, измерении на электрических приборах сравнения с помощью магазинов сопротивлений, емкостей или индуктивностей, измерении объемов жидкостей мерниками меньшей вместимости и так далее. В этих случаях в качестве наиболее достоверной оценки 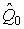истинного значения измеряемой величины Q 0принимается сумма оценок 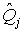истинных значений слагаемых:

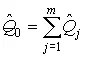. (83)

Пример. Без учета поправки на теплообмен подъем температуры Δ t в калориметре определяют как разность между конечной t 2 и начальной t 1 температурами. После обработки опытных данных были получены следующие (округленные) результаты с соответствующими среднеквадратическими отклонениями:

t 1= 25.10718°C, s i = 0.6·10 -4°C,

t 2= 25.10739°C, s i = 0.3·10 -4°C.

Результат косвенного измерения находим по формуле (74) как разность соответствующих средних арифметических:

,

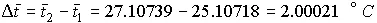а среднеквадратическое отклонение результата по формуле (77):

.

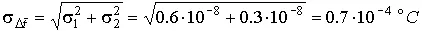Итог измерения:

Δ t = (2.00021±0.00007)°C, P =0.6826.

Здесь мы приняли t p = 1, что при нормальном распределении погрешностей измерений и достаточно большом числе их наблюдений соответствует доверительной вероятности 0.6826 нахождения подъема температуры в указанных пределах.

Не все частные погрешности E k косвенного измерения играют одинаковую роль в формировании итоговой погрешности результата. Так, например, если частные погрешности удовлетворяют неравенству

,

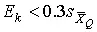то ими можно пренебречь.

Эта формула в метрологии называется критерием ничтожных погрешностей , а сами погрешности, отвечающие условию (78), называются ничтожными или ничтожно малыми .

Использование критерия ничтожных погрешностей при решении задачи косвенных измерений позволяет найти те величины, повышение точности измерения которых позволит уменьшить суммарную погрешность результата. Очевидно, не имеет смысла повышать точность измерения тех величин, частные погрешности которых и без того ничтожно малы.

Все средства измерений, независимо от их конкретного исполнения, обладают рядом общих свойств, необходимых для выполнения ими их функционального назначения. Технические характеристики, описывающие эти свойства и оказывающие влияние на результаты и на погрешности измерений, называются метрологическими характеристиками [9, 10]. Перечень важнейших из них регламентируется ГОСТ “Нормируемые метрологические характеристики средств измерений”. Комплекс нормируемых метрологических характеристик устанавливается таким образом, чтобы с их помощью можно было оценить погрешность измерений, осуществляемых в известных рабочих условиях эксплуатации посредством отдельных средств измерений или совокупности средств измерений, например автоматических измерительных систем.

Одной из основных метрологических характеристик измерительных преобразователей является статическая характеристика преобразования (иначе называемая функцией преобразования или градуировочной характеристикой). Она устанавливает зависимость y = f ( x ) информативного параметра у выходного сигнала измерительного преобразователя от информативного параметра х входного сигнала.

Статическая характеристика нормируется путем задания в форме уравнения, графика или таблицы. Понятие статической характеристики применимо и к измерительным приборам, если под независимой переменной х понимать значение измеряемой величины или информативного параметра входного сигнала, а под зависимой величиной – показание прибора.

Если статическая характеристика преобразования линейна, т.е. y = Kx , то коэффициент K называется чувствительностью измерительного прибора (преобразователя). В противном случае под чувствительностью следует понимать производную от статической характеристики.

Важной характеристикой шкальных измерительных приборов является цена деления , т.е. то изменение измеряемой величины, которому соответствует перемещение указателя на одно деление шкалы. Если чувствительность постоянна в каждой точке диапазона измерения, то шкала называется равномерной . При неравномерной шкале нормируется наименьшая цена деления шкалы измерительных приборов. У цифровых приборов шкалы в явном виде нет, и на них вместо цены деления указывается цена единицы младшего разряда числа в показании прибора.