Всё о метрологии
- Название:Всё о метрологии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Всё о метрологии краткое содержание
Всё о метрологии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности . К их числу относятся:
• погрешности определения поправок;
• погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
• погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы и поправки на них не вводятся.
Для каждого данного измерения элементарные составляющие систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однотипных измерений эти составляющие лежат в определенных границах 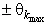 или имеют определенные средние квадратические отклонения
или имеют определенные средние квадратические отклонения 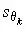 . В первом случае для неисключенных остатков следует принять равномерное распределение, во втором — нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому
. В первом случае для неисключенных остатков следует принять равномерное распределение, во втором — нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому
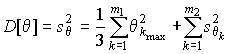 , (63)
, (63)
где m 1— число равномерно распределенных и m 2 — число нормально распределенных элементарных составляющих.
Глава 6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ИСПРАВЛЕННЫХ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Экспериментатор должен быть достаточно ленив, чтоб не делать лишнего
6.1. Обработка результатов прямых равнорассеянных наблюдений
Прямыми называются измерения, в результате которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения осуществляются путем многократных наблюдений. Результаты наблюдений X 1, X 2,…, X n называются равнорассеянными , если они являются независимыми, одинаково распределенными случайными величинами. Равнорассеянные результаты получают при измерениях, проводимых одним наблюдателем или группой наблюдателей с помощью одних и тех же методов и средств измерений в неизменных условиях внешней среды.
Обработка результатов наблюдений в соответствии с методикой прямых измерений с многократными наблюдениями производится в следующем порядке:
1. Путем введения поправок исключают известные систематические погрешности из результатов наблюдений.
2. Вычисляют среднее арифметическое 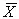 исправленных результатов наблюдений, принимая его за оценку истинного значения измеряемой величины.
исправленных результатов наблюдений, принимая его за оценку истинного значения измеряемой величины.
3. Вычисляют оценку s x среднеквадратического отклонения результатов наблюдения и оценку 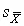 среднеквадратического отклонения среднего арифметического.
среднеквадратического отклонения среднего арифметического.
4. Проверяют гипотезу о нормальности распределения результатов наблюдения. Если число результатов n >50, используют критерий Пирсона χ², при 15< n <50 — составной критерий. Уровень значимости выбирается из интервала 0.02–0.10. При n <15 нормальность распределения не проверяется.
5. Если результаты наблюдений распределены нормально, то определяют наличие грубых погрешностей и промахов и если последние обнаружены, соответствующие результаты отбраковывают и повторяют вычисления.
6. Вычисляют доверительные границы случайной погрешности при доверительной вероятности P =0.95, а также при P =0.99, если измерения в дальнейшем повторить нельзя.
7. Определяют границы неисключенной систематической погрешности результата измерений. В качестве составляющих неисключенной систематической погрешности рассматривают погрешности метода, погрешности средств измерений (например пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение и тогда границы неисключенной систематической погрешности результата при числе составляющих m >4 определяют как
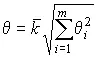 , (64)
, (64)
где θ i — границы отдельных составляющих общим числом m ; k — коэффициент, равный 1.1 при доверительной вероятности P =0.95 и 1.4 при P =0.99.
8. Вычисляют доверительные границы погрешности результата. Если выполняется условие 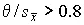 , то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата как доверительные границы случайной погрешности
, то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата как доверительные границы случайной погрешности 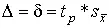 при P =0.95 (и при P =0.99); если же выполняется условие
при P =0.95 (и при P =0.99); если же выполняется условие 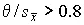 , то можно пренебречь случайной погрешностью и тогда Δ=θ при P =0.95 (и P =0.99).
, то можно пренебречь случайной погрешностью и тогда Δ=θ при P =0.95 (и P =0.99).
Если эти условия не выполняются, то доверительные границы погрешности результата определяют по формуле Δ= K * s Σ, где коэффициент K находят из выражения
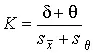 (65)
(65)
а среднеквадратическое общей погрешности результата 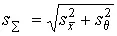 находят квадратическим суммированием дисперсии случайной
находят квадратическим суммированием дисперсии случайной 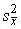 и систематической s ² θ погрешности результата, определяемой формулой (63). Границы случайной δ и систематической θ погрешности, входящие в формулу (65), необходимо выбирать при одной и той же доверительной вероятности ( P =0.95 или P =0.99).
и систематической s ² θ погрешности результата, определяемой формулой (63). Границы случайной δ и систематической θ погрешности, входящие в формулу (65), необходимо выбирать при одной и той же доверительной вероятности ( P =0.95 или P =0.99).
9. Результат измерения записывают в виде  , а при отсутствии сведений о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей — в виде
, а при отсутствии сведений о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей — в виде 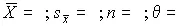 .
.
Если полученный при измерениях результат в дальнейшем используется для анализа и сопоставления с другими результатами или является промежуточным для нахождения других величин, то необходимо указать раздельно границы систематической погрешности и среднеквадратическое отклонение случайной погрешности: 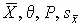 .
.
Интервал:
Закладка:







