Всё о метрологии
- Название:Всё о метрологии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Всё о метрологии краткое содержание
Всё о метрологии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Φ( Z 0.5(1+α))=0.5(1+α)
Величина α находится при заданном уровне значимости q 2второго критерия по данным табл. П.9.
Распределение результатов наблюдения считается отличным от нормального, если оно не соответствует хотя бы одному из этих двух критериев. Уровень значимости составного критерия
q ≤ q 1+ q 2.
При малом числе наблюдений для оценки нормальности можно воспользоваться понятием статистической функции распределения результатов наблюдений . Для ее построения полученные в процессе эксперимента результаты группируют в так называемый вариационный ряд X * (1), X * (2),…, X * (n)члены которого располагаются в порядке их возрастания, так что всегда X * (1)≤ X * (2)≤…≤ X * (n). Статистическую функцию распределения F n ( x k ) определяют по формуле
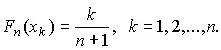 (56)
(56)
F n ( x k ) представляет собой ступенчатую линию, скачки которой соответствуют значениям членов вариационного ряда. Каждый скачок равен 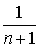 , если все n членов ряда различны. Если же для некоторого k X * ( k )= X * ( k +1)≤…≤ X * ( k+i ), то F n ( x ) в точке x=X k возрастает на
, если все n членов ряда различны. Если же для некоторого k X * ( k )= X * ( k +1)≤…≤ X * ( k+i ), то F n ( x ) в точке x=X k возрастает на 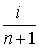 , где i – число равных между собой членов ряда.
, где i – число равных между собой членов ряда.
Если число наблюдений безгранично увеличивать, то статистическая функция распределения сходится по вероятности к истинной функции F n ( x ).
Для проверки нормальности распределения результатов наблюдений по табл.3 приложения находят значения z k , соответствующие полученным значениям F n ( x k ) статистической функции распределения Φ( z k )= F n ( x k ). Но переменная z определяется через результаты наблюдений как
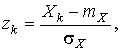
и если в координатах z , x нанести точки z k , x k , то при нормальном распределении они должны расположиться вдоль одной прямой линии. Если же в результате такого построения получится некоторая кривая линия, то гипотезу о нормальности распределения придется отвергнуть как противоречащую опытным данным.
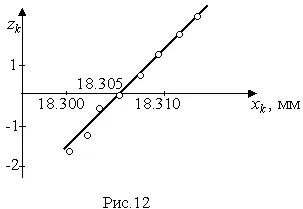
Пример.Даны результаты девятнадцати измерений длины детали (см. табл. 3). Проверить нормальность распределения результатов наблюдений.
Вычисления по изложенной методике сведены в табл.8.
Таблица 8
| x k , мм | F n ( x k )=Φ( z k ) | z k |
|---|---|---|
| 18.303 | 0.05 | -1.6449 |
| 18.304 | 0.10 | -1.2816 |
| 18.305 | 0.20 | -0.8416 |
| 18.306 | 0.30 | -0.5244 |
| 18.307 | 0.40 | -0.2533 |
| 18.308 | 0.60 | 0.2533 |
| 18.309 | 0.75 | 0.6745 |
| 18.310 | 0.85 | 1.0364 |
| 18.311 | 0.90 | 1.2816 |
| 18.312 | 0.95 | 1.6449 |
На рис. 12 представлена зависимость z k (x k). Отдельные точки располагаются очень близко к прямой, поэтому распределение результатов наблюдений можно считать нормальным.
4.8. Обнаружение грубых погрешностей
В начале главы уже было отмечено, что грубыми называют погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента. Для их устранения желательно еще перед измерениями определить значение искомой величины приближенно, с тем чтобы в дальнейшем можно было сконцентрировать внимание лишь на уточнении предварительных данных. Если оператор в процессе измерений обнаруживает, что результат одного из наблюдений резко отличается от других, и находит причины этого, то он, конечно, вправе отбросить этот результат и провести повторные измерения. Но необдуманное отбрасывание резко отличающихся от других результатов может привести к существенному искажению характеристик рассеивания ряда измерений, поэтому повторные измерения лучше проводить не взамен сомнительных, а в дополнение к ним.
Особенно остро ставится вопрос об устранении грубых погрешностей при обработке уже имеющегося материала, когда невозможно учесть все обстоятельства, при которых проводили измерения. В этом случае приходится прибегать к чисто статистическим методам.
Вопрос о том, содержит ли данный результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез.
Проверяемая гипотеза состоит в утверждении, что результат наблюдения X i не содержит грубой погрешности, т.е. является одним из значений случайной величины Х с законом распределения F X ( x ), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший X max или наименьший X minиз результатов наблюдений. Поэтому для проверки гипотезы следует воспользоваться распределениями величин
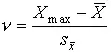 или
или 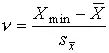 . (57)
. (57)
Функции их распределения определяют методами теории вероятностей [3]. Они совпадают между собой и для нормального распределения результатов наблюдений протабулированы и представлены в табл. П.7 приложения. По данным этой таблицы, при заданной доверительной вероятности α или уровне значимости q =1–α можно для количества измерения n =3–25 найти те наибольшие значения ν a , которые случайная величина ν может еще принять по чисто случайным причинам.
Если вычисленное по опытным данным значение ν окажется меньше ν a , то гипотеза принимается; в противном случае ее следует отвергнуть как противоречащую данным наблюдений. Тогда результат X max или соответственно X minприходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений.
Глава 5. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
Наука начинается там, где начинается классификация.
5.1. Классификация систематических погрешностей
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины [15, 17]. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалов, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.
Читать дальшеИнтервал:
Закладка:







