Всё о метрологии

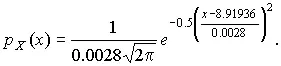
Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе?

Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению F X ( x ) с плотностью P X ( x ).

Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U , представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами:

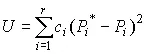(52)

где t p — коэффициенты, называемые весами разрядов; P i — теоретические вероятности, определяемые как

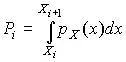, (53)

Здесь p X ( x ) — предполагаемая плотность распределения.

Мера расхождения U является случайной величиной и, независимо от исходного распределения подчиняется χ²-распределению с k степенями свободы — см. формулу (44). Если значения всех частот m i >5, число измерений стремится к бесконечности, а веса c i выбираются равными n / P i . Число степеней свободы распределения k = r–s , где r — число разрядов гистограммы статистического распределения, а s — число независимых связей, наложенных на частости P i *.

Если проверяется гипотеза о нормальности распределения, то к числу этих связей относится равенство среднего арифметического математическому ожиданию, а точечной оценки дисперсии - дисперсии предполагаемого нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей по всем интервалам была равна единице. Поэтому в данном случае s = 3.

По табл. П.6 можно при заданной доверительной вероятности α=1- q найти тот доверительный интервал (χ² k ,0.5 q , χ² k ,1-0.5 q ) значений χ² k , в который мера расхождения может попасть по чисто случайным причинам.

Если вычисленная по опытным данным мера расхождения окажется в указанном интервале, то гипотеза принимается. Это, конечно, не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. не противоречит опытным данным. Если же она выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.

Поскольку проверка гипотезы основывается на опытных данных, то при принятии решения всегда возможны ошибки. Отвергая в действительности верную гипотезу, мы совершаем ошибку первого рода . Вероятность ошибки первого рода называется уровнем значимости и составляет q =1- a . Принимая в действительности неверную гипотезу, мы совершаем ошибку второго рода . Вычислить ее вероятность, вообще говоря, невозможно, поскольку для этого нужно рассмотреть все прочие возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь утверждать, что при уменьшении ошибки первого рода ошибка второго рода увеличивается, поэтому не имеет смысла брать слишком высокие значения доверительных вероятностей.

Описанная процедура проверки гипотезы о том, что данное статистическое распределение является распределением с плотностью p X ( x ), называется критерием согласия χ². Проверка нормальности распределения согласно критерию χ² сводится к следующему.

1. Данные наблюдений группируют по интервалам, как при построении гистограммы, и подсчитывают частоты m i . Если в некоторые интервалы попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними. При этом число степеней свободы k , конечно, уменьшается.

2. Вычисляют среднее арифметическое 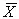и точечную оценку среднеквадратического отклонения результата наблюдений s X , которые принимают в качестве параметров теоретического нормального распределения с плотностью p X ( x ).

3. Для каждого интервала находят вероятности попадания в них результатов наблюдений либо по общей формуле (29), либо приближенно как произведение плотности теоретического распределения в середине интервала на его длину:

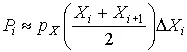. (54)

4. Для каждого интервала вычисляют величины χ² i ( i =1,2,…, r ) и суммируют их по всем i , в результате чего получают меру расхождения χ².

5. Определяют число степеней свободы k=r -3 и, задаваясь уровнем значимости q =1- a , находят по табл. П.6 приложения значения χ² k ,0.5 q и (χ² k ,0.5 q , χ² k ,1-0.5 q ). Если χ² k ,0.5 q < χ² k < χ² k ,1-0.5 q , то распределение результатов наблюдений считают нормальным.

Критерий согласия χ² k , построенный на предельном переходе при n →∞, рекомендуется применять, если общее число наблюдений больше сорока.

При малом числе наблюдений 11< n <50 нормальность распределения результатов наблюдений проверяется с помощью двух критериев.

Первый критерий основан на вычислении статистики

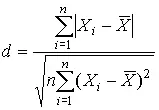. (55)

Гипотеза о нормальности распределения на основании первого критерия принимается, если при данном числе наблюдений и выбранном уровне значимости q 1соблюдается условие

,

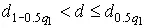где 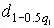и 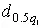— квантили, выбираемые из табл. П.8.

На основании второго критерия гипотеза о нормальности распределения принимается, если не более m разностей 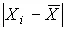превосходят уровень s XZ 0.5(1+α), где s X — оценка среднеквадратического отклонения результатов наблюдения, Z 0.5(1+α) — квантиль интегральной функции нормированного нормального распределения, определяемый по данным табл. П.2 приложения при значении