Всё о метрологии

что уже позволяет сделать некоторые выводы относительно точности проведенных измерений.

Наряду с методом максимального правдоподобия при определении точечных оценок широко используется метод наименьших квадратов . В соответствии с этим методом среди некоторого класса оценок выбирают ту, которая обладает наименьшей дисперсией, т. е. наиболее эффективную оценку. Легко заметить, что среди всех линейных оценок истинного значения вида 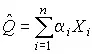, где α i — некоторые постоянные, именно среднее арифметическое 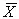обращает в минимум дисперсию 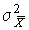. Поэтому для случая нормально распределенных случайных погрешностей оценки, получаемые методом наименьших квадратов, совпадают с оценками максимального правдоподобия.

Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными , между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров.

Вначале остановимся на определении доверительного интервала для среднего арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия σ² X . Найдем вероятность попадания результата наблюдений в интервал 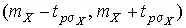. Согласно формуле (29)

Но

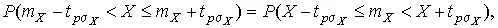
и, если систематические погрешности исключены ( m X = Q ),

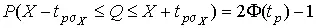(34)

Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью P =2Φ( t p )–1 находится между границами доверительного интервала .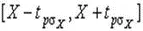

Половина длины доверительного интервала 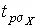называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р . Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р =0.95 или Р =0.995 и по формулам

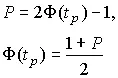(35)

определяют соответствующее значение Φ( t p ) интегральной функции нормированного нормального распределения. Затем по данным табл. П.3 приложения находят значение коэффициента t p и вычисляют доверительное отклонение 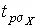. Проведение многократных наблюдений позволяет значительно сократить доверительный интервал. Действительно, если результаты наблюдений X i ( i =1, 2,..., n ) распределены нормально, то нормально распределены и величины X i / n , а значит, и среднее арифметическое 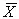, являющееся их суммой. Поэтому имеет место равенство

(36)

где t p определяется по заданной доверительной вероятности Р .

Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в √ n раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.

Половина длины нового доверительного интервала

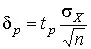(37)

называется доверительной границей погрешности результата измерений , а итог измерений записывается в виде

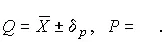(38)

Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением

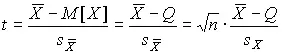(39)

называемым дробью Стьюдента . Входящие в нее величины 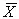и s X вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.

Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:

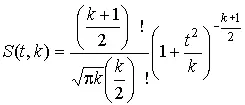(40)

где S ( t , k ) — плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n – 1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (– t p , + t p ), согласно выражению (8), вычисляется по формуле

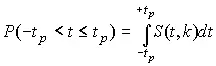
или, поскольку S ( t , k ) является четной функцией аргумента t ,

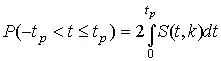
Подставив вместо дроби Стьюдента t ее выражение через 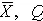и 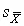, получим окончательно

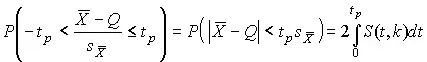(41)

Величины t p , вычисленные по формулам (40) и (41), были табулированы Фишером для различных значений доверительной вероятности Р в пределах 0.10–0.99 при k = n –1 = 1,2,…,30. В табл. П.5 приведены значения t p для наиболее часто употребляемых доверительных вероятностей Р .