Всё о метрологии

Для выявления вида наиболее вероятных распределений рассмотрим несколько наиболее типичных случаев [3].

1. В классе распределений результатов наблюдений p X ( x ), обладающих определенной зоной рассеивания между значениями х = b и х = а шириной b-а = 2а , найдем такое, которое обращает в максимум энтропию 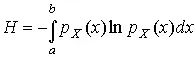при наличии ограничивающих условий:

p X ( x ) > 0, , ,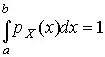

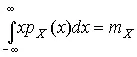где 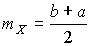— математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.

Искомая плотность распределения результатов наблюдений описывается выражением

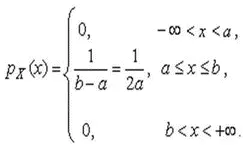(23)

Такое распределение результатов наблюдений называется равномерным .

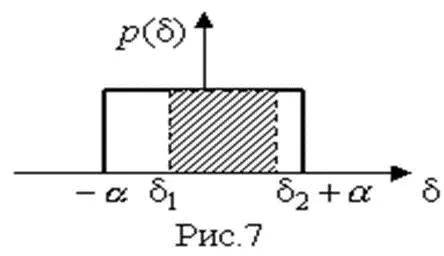
Значения дифференциальной функции распределения равномерной распределенной случайной погрешности постоянны в интервале [– а ; + а ], а вне этого интервала равны нулю (рис.6).

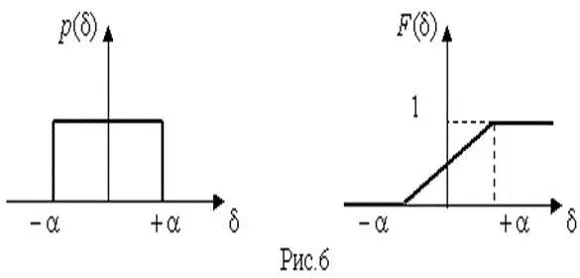
Поэтому выражение для дифференциальной функции распределения случайной погрешности можно записать в виде

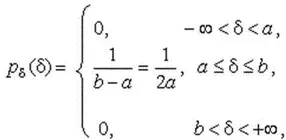(24)

Определим числовые характеристики равномерного распределения. Математическое ожидание случайной погрешности находим по формуле (10):

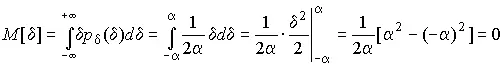
Дисперсию случайной равномерно распределенной погрешности можно найти по формуле (18):

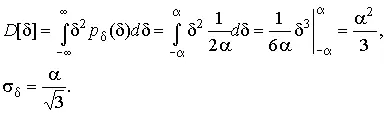
В силу симметрии распределения относительно математического ожидания коэффициент асимметрии должен равняться нулю:

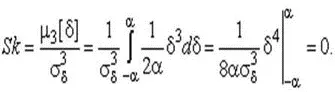
Для определения эксцесса найдем вначале четвертый момент случайной погрешности:

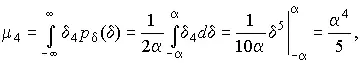
поэтому

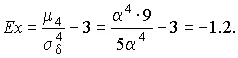
В заключение найдем вероятность попадания случайной погрешности в заданный интервал [δ 1, δ 2], равный заштрихованной площади на рис. 7.

2. В классе распределений результатов наблюдений p X ( x ), обладающих определенной дисперсией σ² X , найдем такое, которое обращает в максимум энтропию 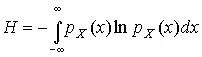при наличии ограничений:

p X ( x ) > 0, , , .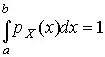

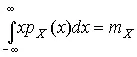Решение этой задачи также находится методом множителей Лагранжа. Искомая плотность распределения результатов наблюдений описывается выражением

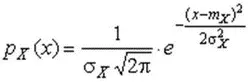(25)

где m X — математическое ожидание и σ² X — среднеквадратическое отклонение результатов наблюдений.

Учитывая, что при полном исключении систематических погрешностей x–m X =δ и σ X=σ δ, для дифференциальной функции распределения случайной погрешности можно записать уравнение

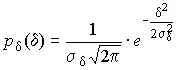(25)

Распределение, описываемое уравнениями (25) и (26), называется нормальным или распределением Гаусса .

На рис.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения (σ 1> σ 2> σ 3).

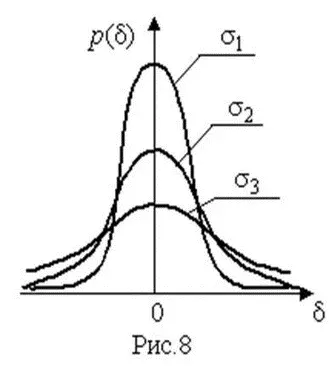
Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

Вычислим вероятность попадания результата наблюдения в некоторый заданный интервал (x 1, x 2]:

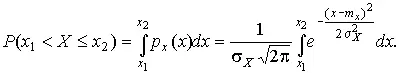
Заменим переменные:

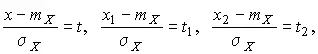
после чего получим следующее выражение для искомой вероятности:

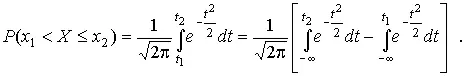
Интегралы, стоящие в квадратных скобках, не выражаются в элементарных функциях, поэтому их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией

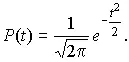(27)

В приложении (табл. П. 5 и П. 6) приведены значения дифференциальной функции нормированного нормального распределения, а также интегральной функции этого распределения, определяемой как

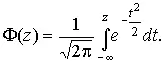(28)

С помощью функции Ф( z ) вероятность P ( x 1< X ≤ x 2) находят как

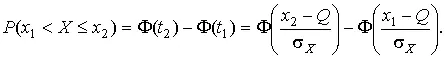(29)

При использовании данной формулы следует иметь в виду тождество

Φ(z) ≡ 1-Φ(–z)

вытекающее непосредственно из определения функции Ф( z ).