Всё о метрологии
- Название:Всё о метрологии
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Всё о метрологии краткое содержание
Всё о метрологии - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
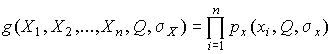 (31)
(31)
достигает наибольшего значения. Постоянный сомножитель Δ x n не оказывает влияния на решение и поэтому может быть отброшен. Полученные оценки  и
и  истинного значения и среднеквадратического отклонения называются о ценками максимального правдоподобия .
истинного значения и среднеквадратического отклонения называются о ценками максимального правдоподобия .
Для упрощения вычислений иногда бывает удобнее пользоваться логарифмической функцией правдоподобия
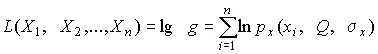 (32)
(32)
Если наибольшее значение функции правдоподобия совпадает с максимальным значением, то оценки получаются из системы уравнений
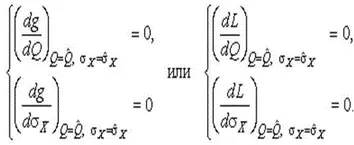 (33)
(33)
В противном случае необходимо более подробное исследование функции правдоподобия.
Далее определим оценки максимального правдоподобия для трех распределений случайных погрешностей, представленных в предыдущей главе.
1. Результаты наблюдений распределены нормально. В этом случае

а логарифмическая функция правдоподобия в соответствии с (32)
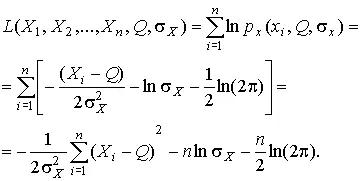
Система уравнений (33) приводится к виду
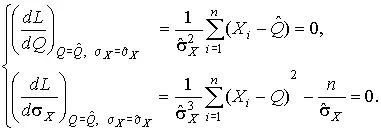
Из первого уравнения получаем выражение для оценки истинного значения  , а из второго — оценку среднеквадратического отклонения
, а из второго — оценку среднеквадратического отклонения 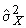 :
:
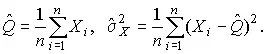
Таким образом, при нормальном распределении случайных погрешностей оценкой максимального правдоподобия для истинного значения является среднее арифметическое из результатов отдельных наблюдений, а оценкой дисперсии — среднее из квадратов отклонений результатов наблюдений от среднего арифметического.
2. Результаты наблюдений распределены по закону Лапласа
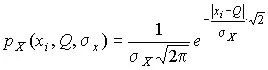
Логарифмическая функция правдоподобия не является дифференцируемой по Q , поэтому приходится прибегать к численным методам, функция правдоподобия достигает наибольшего значения, когда выражение 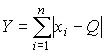 принимает наименьшее значение. Поэтому задача об отыскании оценки истинного значения сводится к определению такого значения
принимает наименьшее значение. Поэтому задача об отыскании оценки истинного значения сводится к определению такого значения 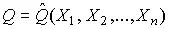 , сумма модулей отклонений результатов наблюдений от которого является наименьшей. Задача решается методом последовательных приближений, причем в качестве первого приближения можно принять среднее арифметическое из полученных результатов.
, сумма модулей отклонений результатов наблюдений от которого является наименьшей. Задача решается методом последовательных приближений, причем в качестве первого приближения можно принять среднее арифметическое из полученных результатов.
3. В условиях равномерного распределения погрешностей
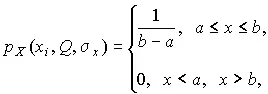
причем a = Q –σ X √3 и b = Q +σ X √3.
Решение задачи нахождения оценки максимального правдоподобия для равномерного распределения погрешностей проводим численными методами, в результате чего получаем:
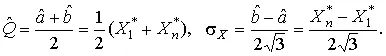
Основное достоинство оценок максимального правдоподобия в том, что они являются асимптотически (при n →∞) несмещенными; асимптотически эффективными и асимптотически нормально распределенными.
Если â — оценка максимального правдоподобия для параметра а , то при достаточно большом числе n наблюдений (практически уже при n >20-25) эту оценку можно считать нормально распределенной с математическим ожиданием M [ â ]= a и дисперсией D [ â ]=( M [–∂ 2 L /∂ a 2]) -1 при любом распределении результатов наблюдений.
Для наиболее часто встречающегося на практике нормального распределения случайных погрешностей оценки максимального правдоподобия имеются особые обозначения.
Оценкой истинного значения является среднее арифметическое 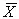 из результатов отдельных наблюдений X i ,
из результатов отдельных наблюдений X i ,
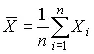 .
.
Вторая производная от логарифмической функции преобразования равна ∂² L /∂ Q ² = – n /σ² X , поэтому дисперсия среднего арифметического в n раз меньше дисперсии σ² X результатов наблюдений, т. е.
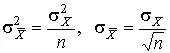 .
.
Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как
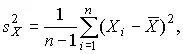
а оценку среднеквадратического отклонения результатов наблюдений как
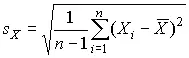
Дисперсия оценки s X среднеквадратического отклонения составляет
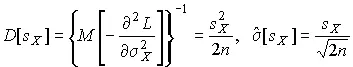 .
.
Последнее соотношение показывает, что относительная погрешность определения среднеквадратического отклонения (в %) по результатам обработки ряда наблюдений достаточно велика:
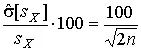
и даже при n = 50 достигает 10%. Для надежного суждения о точности эту погрешность следует увеличить еще минимум в два раза.
С помощью полученных оценок итог измерений можно записать в виде
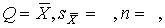
Интервал:
Закладка:







